Question
Question: $\lim_{x \to 2024} \sqrt[1]{(x-2023)^{2023}(x-2024)^{2024}\cdot (x-2025)^{2025}}$...
limx→20241(x−2023)2023(x−2024)2024⋅(x−2025)2025
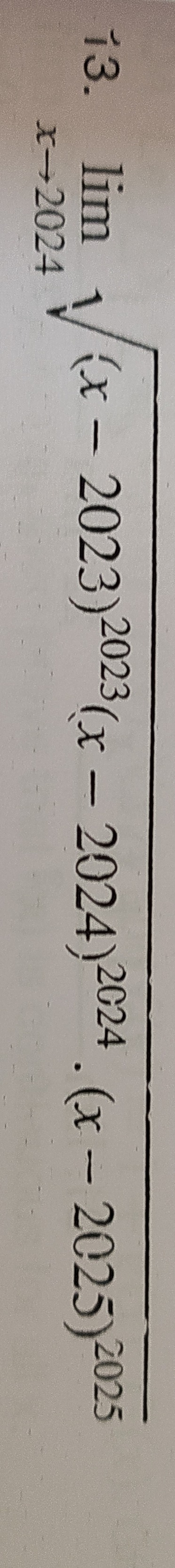
0
Solution
The given limit is limx→20241(x−2023)2023(x−2024)2024⋅(x−2025)2025.
The notation 1y represents the first root of y, which is y1/1=y.
So, the expression simplifies to (x−2023)2023(x−2024)2024⋅(x−2025)2025.
Let f(x)=(x−2023)2023(x−2024)2024⋅(x−2025)2025.
This function is a product of terms of the form (x−a)n, where n is a positive integer. Such terms are polynomials in x. The product of polynomials is a polynomial.
Polynomial functions are continuous for all real numbers.
Since f(x) is a polynomial, it is continuous at x=2024.
For a continuous function, the limit as x approaches a point is equal to the function value at that point.
Therefore, limx→2024f(x)=f(2024).
Substitute x=2024 into the expression for f(x):
f(2024)=(2024−2023)2023(2024−2024)2024⋅(2024−2025)2025
f(2024)=(1)2023(0)2024⋅(−1)2025
Evaluate each term:
(1)2023=1
(0)2024=0 (since the exponent is positive, 0n=0 for n>0)
(−1)2025=−1 (since the exponent is odd, (−1)n=−1 for odd n)
Now, multiply the results:
f(2024)=1⋅0⋅(−1)=0.
Thus, the limit of the function as x→2024 is 0.
