Question
Question: Let $n \geq 2$ be a natural number and $0 < \theta < \pi/2$. Then $\int \frac{(\sin^n \theta - \sin ...
Let n≥2 be a natural number and 0<θ<π/2. Then ∫sinn+1θ(sinnθ−sinθ)n1cosθdθ is equal to: (2019)
(where C is a constant of integration)
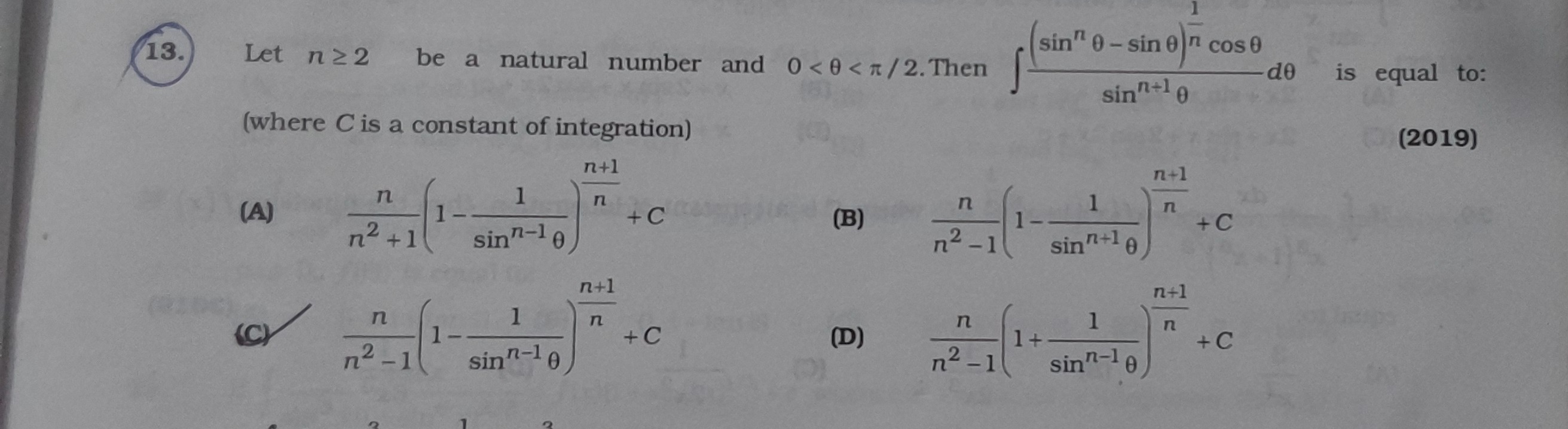
n2+1n(1−sinn−1θ1)nn+1+C
n2−1n(1−sinn−1θ1)nn+1+C
n2−1n(1−sinn−1θ1)nn+1+C
n2−1n(1+sinn−1θ1)nn+1+C
n2−1n(1−sinn−1θ1)nn+1+C
Solution
The given integral is I=∫sinn+1θ(sinnθ−sinθ)n1cosθdθ.
Step 1: Simplify the term inside the parenthesis in the numerator.
Factor out sinnθ from (sinnθ−sinθ): sinnθ−sinθ=sinnθ(1−sinnθsinθ)=sinnθ(1−sinn−1θ1).
Now, raise this to the power of n1: (sinnθ−sinθ)n1=(sinnθ(1−sinn−1θ1))n1 =(sinnθ)n1(1−sinn−1θ1)n1 =sinθ(1−sinn−1θ1)n1.
Step 2: Substitute this simplified term back into the integral. I=∫sinn+1θsinθ(1−sinn−1θ1)n1cosθdθ I=∫sinnθ(1−sinn−1θ1)n1cosθdθ.
Step 3: Use substitution. Let t=1−sinn−1θ1. This can be written as t=1−(sinθ)−(n−1). Now, differentiate t with respect to θ: dθdt=0−(−(n−1))(sinθ)−(n−1)−1(cosθ) dθdt=(n−1)(sinθ)−ncosθ dθdt=(n−1)sinnθcosθ.
From this, we can express sinnθcosθdθ in terms of dt: sinnθcosθdθ=n−11dt.
Step 4: Substitute t and dt into the integral. I=∫tn1(n−11)dt I=n−11∫tn1dt.
Step 5: Integrate with respect to t. I=n−11(n1+1tn1+1)+C I=n−11(nn+1tnn+1)+C I=n−11(n+1ntnn+1)+C I=(n−1)(n+1)ntnn+1+C I=n2−1ntnn+1+C.
Step 6: Substitute back t=1−sinn−1θ1. I=n2−1n(1−sinn−1θ1)nn+1+C.
Comparing this result with the given options, option (B) and (C) are identical and match our derived solution.
