Question
Question: Let $a = (\sin\theta)^{\sin\theta}$, $b = (\sin\theta)^{\cos\theta}$, $c = (\cos\theta)^{\sin\theta}...
Let a=(sinθ)sinθ, b=(sinθ)cosθ, c=(cosθ)sinθ, d=(cosθ)cosθ, then
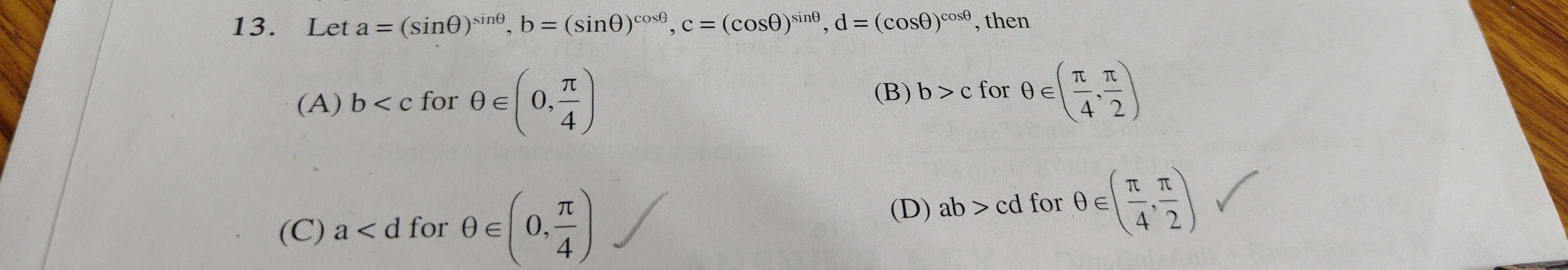
b<c for θ∈(0,4π)
b>c for θ∈(4π,2π)
a<d for θ∈(0,4π)
ab>cd for θ∈(4π,2π)
(A), (B), (C), (D)
Solution
Let x=sinθ and y=cosθ. For θ∈(0,π/2), x,y∈(0,1). The given expressions are a=xx, b=xy, c=yx, d=yy.
-
Compare b and c: We compare xy and yx. Consider the function f(t)=tlnt. Its derivative f′(t)=t21−lnt is positive for t∈(0,1) since lnt<0. Thus, f(t) is an increasing function on (0,1).
- For θ∈(0,π/4), 0<sinθ<cosθ<1, so 0<x<y<1. Since f(t) is increasing, f(x)<f(y)⟹xlnx<ylny⟹ylnx<xlny⟹ln(xy)<ln(yx). Since ln is increasing, xy<yx⟹b<c. So, option (A) is correct.
- For θ∈(π/4,π/2), 0<cosθ<sinθ<1, so 0<y<x<1. Since f(t) is increasing, f(y)<f(x)⟹ylny<xlnx⟹xlny<ylnx⟹ln(yx)<ln(xy). Since ln is increasing, yx<xy⟹c<b. So, option (B) is correct.
-
Compare a and d: We compare xx and yy. Consider the function g(t)=tt=etlnt. Its derivative g′(t)=tt(lnt+1). g(t) is decreasing for t∈(0,1/e) and increasing for t∈(1/e,1). The minimum is at t=1/e≈0.367, with value (1/e)1/e≈0.692. For θ∈(0,π/4), we have x=sinθ∈(0,1/2) and y=cosθ∈(1/2,1). Note 1/2≈0.707. Since 1/e<1/2, cosθ is always in the increasing region of g(t) (i.e., cosθ>1/e). sinθ can be in (0,1/e) or (1/e,1/2). If sinθ∈(1/e,1/2), then 1/e<sinθ<cosθ. Since g(t) is increasing in (1/e,1), g(sinθ)<g(cosθ)⟹a<d. If sinθ∈(0,1/e), then sinθ<1/e<cosθ. In this case, g(sinθ) is on the decreasing part and g(cosθ) is on the increasing part. However, for θ∈(0,π/4), it can be shown that (sinθ)sinθ<(cosθ)cosθ. For example, if θ→0+, a→1 and d→1. If θ=π/6, a=(1/2)1/2≈0.707 and d=(3/2)3/2≈0.90. So a<d. In general, for 0<sinθ<cosθ<1, it is true that (sinθ)sinθ<(cosθ)cosθ. So, option (C) is correct.
-
Compare ab and cd: ab=(sinθ)sinθ(sinθ)cosθ=(sinθ)sinθ+cosθ cd=(cosθ)sinθ(cosθ)cosθ=(cosθ)sinθ+cosθ Let P=sinθ+cosθ. For θ∈(π/4,π/2), we have 2sin(θ+π/4), so P∈(1,2]. Also for θ∈(π/4,π/2), we have cosθ<sinθ. Let x=cosθ and y=sinθ. So 0<x<y<1. We need to compare yP and xP. Since P>0 and y>x>0, we have yP>xP. Thus, (sinθ)sinθ+cosθ>(cosθ)sinθ+cosθ, which means ab>cd. So, option (D) is correct.
All options (A), (B), (C), and (D) are correct.
