Question

$\int \frac{\log_e x}{x\sqrt{1+\log_e x}}dx=$

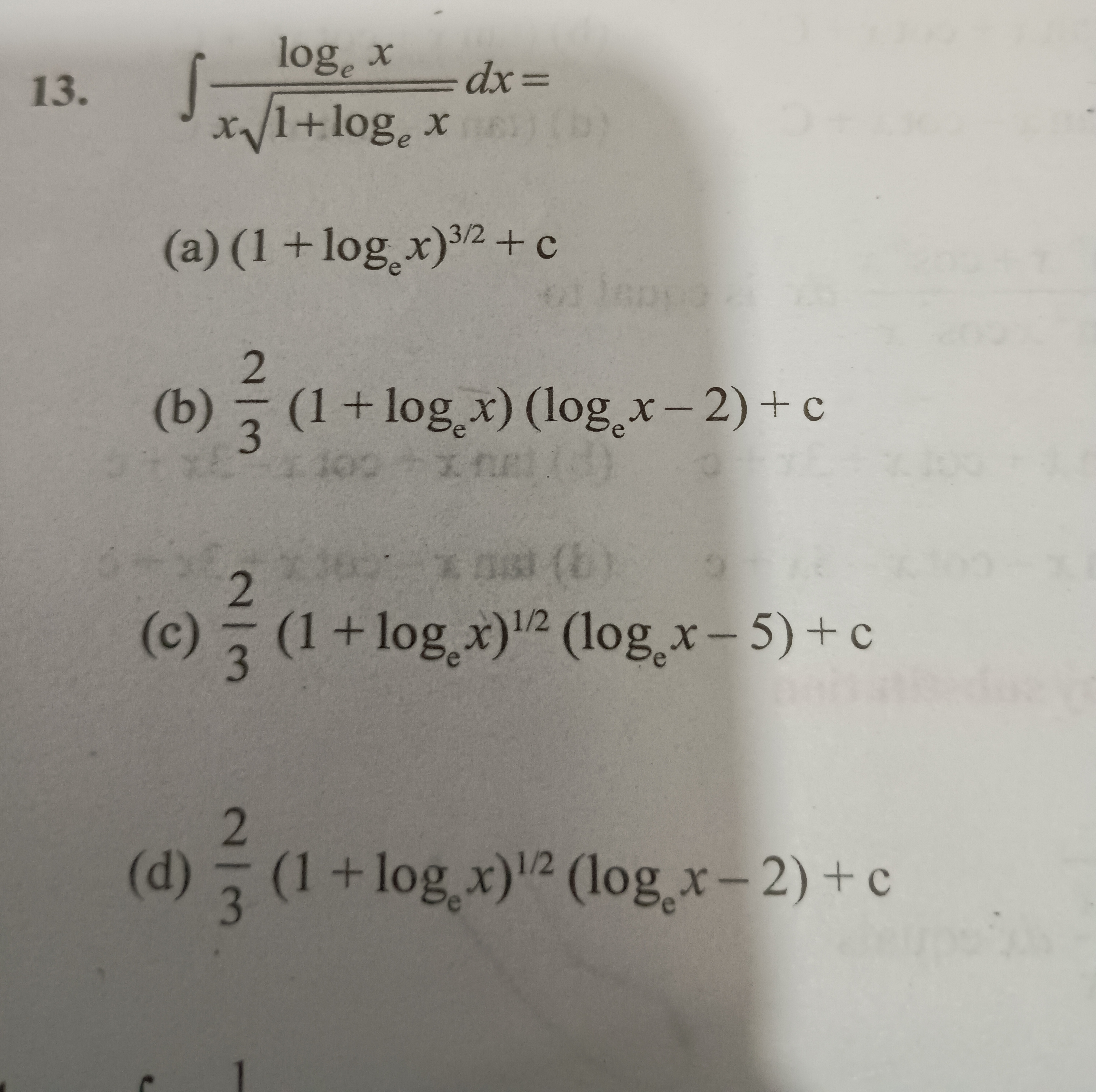
• A. $(1+\log_e x)^{3/2} + c$
• B. $\frac{2}{3} (1 + \log_e x) (\log_e x - 2) + c$
• C. $\frac{2}{3} (1+\log_e x)^{1/2} (\log_e x - 5) + c$
• D. $\frac{2}{3} (1+\log_e x)^{1/2} (\log_e x - 2) + c$

Answer 1

Answer: (D)

(d) $\frac{2}{3} (1+\log_e x)^{1/2} (\log_e x - 2) + c$

Answer 2

The given integral is $\int \frac{\log_e x}{x\sqrt{1+\log_e x}}dx$.

To solve this integral, we use the method of substitution. Let $t = 1 + \log_e x$. Differentiating both sides with respect to $x$, we get: $dt = \frac{1}{x} dx$

From the substitution, we can also express $\log_e x$ in terms of $t$: $\log_e x = t - 1$

Now, substitute these into the integral: $\int \frac{\log_e x}{x\sqrt{1+\log_e x}}dx = \int \frac{t-1}{\sqrt{t}} dt$

We can split the integrand into two terms: $\int \left( \frac{t}{\sqrt{t}} - \frac{1}{\sqrt{t}} \right) dt$ $\int \left( t^{1 - 1/2} - t^{-1/2} \right) dt$ $\int \left( t^{1/2} - t^{-1/2} \right) dt$

Now, integrate each term using the power rule for integration, $\int u^n du = \frac{u^{n+1}}{n+1} + C$: $\frac{t^{1/2 + 1}}{1/2 + 1} - \frac{t^{-1/2 + 1}}{-1/2 + 1} + C$ $\frac{t^{3/2}}{3/2} - \frac{t^{1/2}}{1/2} + C$ $\frac{2}{3} t^{3/2} - 2 t^{1/2} + C$

Now, substitute back $t = 1 + \log_e x$ into the expression: $\frac{2}{3} (1 + \log_e x)^{3/2} - 2 (1 + \log_e x)^{1/2} + C$

To match the options, we can factor out common terms. The common term is $\frac{2}{3} (1 + \log_e x)^{1/2}$: $\frac{2}{3} (1 + \log_e x)^{1/2} \left[ (1 + \log_e x) - \frac{2 \cdot 3}{2} \right] + C$ $\frac{2}{3} (1 + \log_e x)^{1/2} \left[ (1 + \log_e x) - 3 \right] + C$ $\frac{2}{3} (1 + \log_e x)^{1/2} \left[ \log_e x + 1 - 3 \right] + C$ $\frac{2}{3} (1 + \log_e x)^{1/2} (\log_e x - 2) + C$

Comparing this result with the given options, it matches option (d).

The final answer is $\boxed{\text{(d)}}$.

Explanation of the solution: The integral is solved using substitution. Let $t = 1 + \log_e x$, which implies $dt = \frac{1}{x} dx$ and $\log_e x = t - 1$. Substituting these into the integral transforms it into $\int \frac{t-1}{\sqrt{t}} dt$. This simplifies to $\int (t^{1/2} - t^{-1/2}) dt$. Integrating term by term yields $\frac{2}{3} t^{3/2} - 2 t^{1/2} + C$. Finally, substitute $t = 1 + \log_e x$ back and factor the expression to get $\frac{2}{3} (1 + \log_e x)^{1/2} (\log_e x - 2) + C$.