Question
Question: If $x^2 \alpha+y^2 +2\beta y =a^2$ represents a pair of perpendicular lines, then $|\frac{\beta}{\al...
If x2α+y2+2βy=a2 represents a pair of perpendicular lines, then ∣αβ∣=
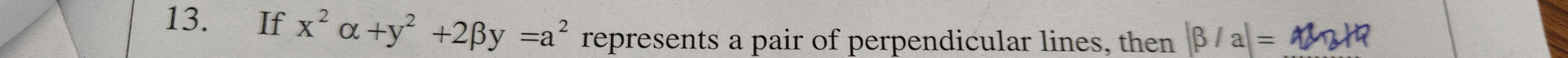
0
1
a
βa2
0
Solution
The general equation of a second-degree curve is Ax2+2Hxy+By2+2Gx+2Fy+C=0. The given equation is αx2+y2+2βy−a2=0. Comparing the coefficients, we have: A=α H=0 B=1 G=0 F=β C=−a2
For the equation to represent a pair of perpendicular lines, the condition is A+B=0. Substituting the values of A and B: α+1=0 ⟹α=−1.
For the equation to represent a pair of lines, the discriminant must be zero: Δ=ABC+2FGH−AF2−BG2−CH2=0. Substituting the coefficients: Δ=(α)(1)(−a2)+2(β)(0)(0)−(α)(β)2−(1)(0)2−(−a2)(0)2=0 Δ=−αa2−αβ2=0 Δ=−α(a2+β2)=0.
Since α=−1, we substitute this into the discriminant equation: −(−1)(a2+β2)=0 1(a2+β2)=0 a2+β2=0.
Assuming a and β are real numbers, the equation a2+β2=0 implies that a2=0 and β2=0. This means a=0 and β=0.
The question asks for the value of ∣αβ∣. ∣αβ∣=∣−10∣=0.
