Question
Question: If $\tan^3 A + \tan^3 B + \tan^3 C = 3 \tan A \tan B \tan C$, then find the value of A + B + C....
If tan3A+tan3B+tan3C=3tanAtanBtanC, then find the value of A + B + C.
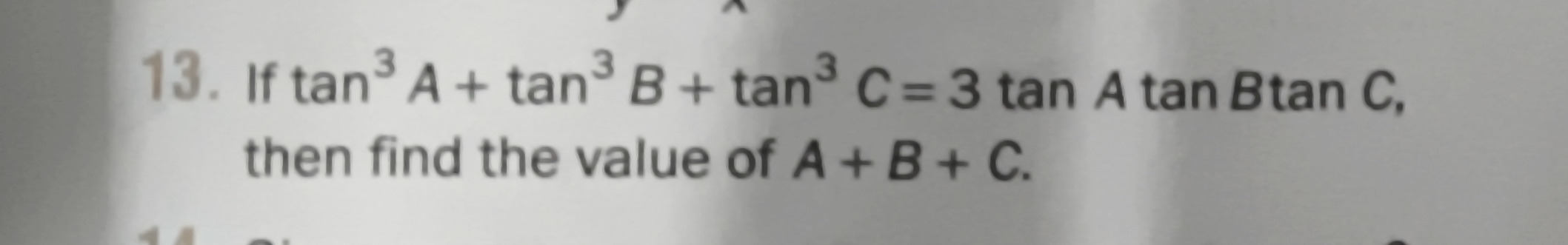
π/2
π
2π
3π/2
π
Solution
Let x=tanA, y=tanB, and z=tanC. The given equation is x3+y3+z3=3xyz. We use the algebraic identity: x3+y3+z3−3xyz=(x+y+z)(x2+y2+z2−xy−yz−zx)
The given condition x3+y3+z3=3xyz implies x3+y3+z3−3xyz=0. Thus, we have: (x+y+z)(x2+y2+z2−xy−yz−zx)=0
This equation holds if either:
- x+y+z=0
- x2+y2+z2−xy−yz−zx=0
The second condition can be rewritten as 21((x−y)2+(y−z)2+(z−x)2)=0, which implies x=y=z.
So, we have two possibilities: a) tanA+tanB+tanC=0 b) tanA=tanB=tanC
In the context of problems like this, where a unique value for A+B+C is expected, it is usually implied that A,B,C are the angles of a triangle. For the angles of a triangle, A+B+C=π.
If A+B+C=π, then it is a known trigonometric identity that: tanA+tanB+tanC=tanAtanBtanC (provided none of the angles are π/2).
Let's examine our conditions in light of A+B+C=π:
Case 1: tanA+tanB+tanC=0 If A+B+C=π, then tanA+tanB+tanC=tanAtanBtanC. If tanA+tanB+tanC=0, then tanAtanBtanC must also be 0. This implies at least one of tanA,tanB,tanC is 0. If tanA=0, then A=kπ for some integer k. Since A is an angle of a triangle, A=0. If A=0, then B+C=π. The condition tanA+tanB+tanC=0 becomes 0+tanB+tanC=0, so tanB=−tanC. This is true if B+C=π. For example, A=0,B=π/4,C=3π/4. Here A+B+C=π.
Case 2: tanA=tanB=tanC If A,B,C are angles of a triangle, and tanA=tanB=tanC, then A=B=C. Since A+B+C=π, we have 3A=π, which means A=π/3. So, A=B=C=π/3. In this case, A+B+C=π.
Both cases, under the assumption that A,B,C are angles of a triangle, lead to A+B+C=π. If we do not assume A,B,C are angles of a triangle, the sum A+B+C can take infinitely many values. However, the question asks for "the value", implying a unique answer, which points to the standard interpretation of A,B,C as angles of a triangle.
Therefore, the value of A+B+C is π.
