Question
Question: If $D_r = \begin{vmatrix} r & 2012 & 2013 \\ 11r^2 & 3r & r \\ r & \frac{1}{r} & \frac{1}{r^2} \end{...
If Dr=r11r2r20123rr12013rr21, then ∑r=15Dr is equal to-
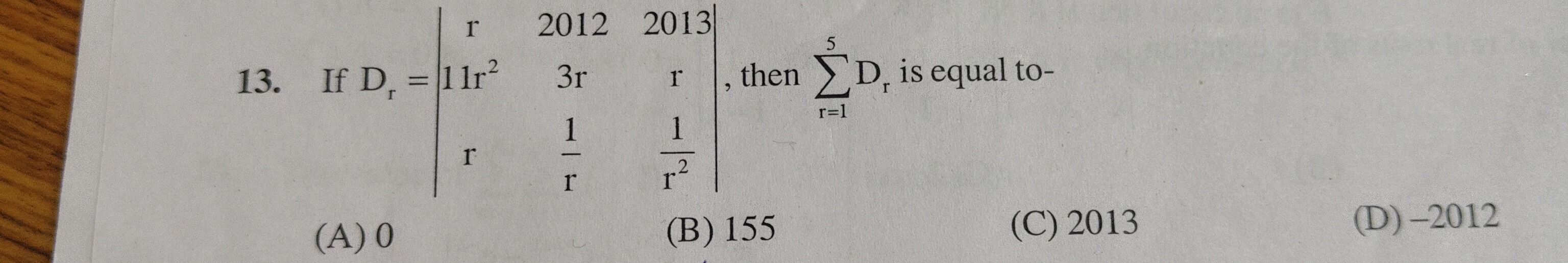
0
155
2013
-2012
0
Solution
To solve the problem, we first need to evaluate the determinant Dr. The given determinant is: Dr=r11r2r20123rr12013rr21
We can expand the determinant along the first row: Dr=r((3r)(r21)−(r)(r1))−2012((11r2)(r21)−(r)(r))+2013((11r2)(r1)−(3r)(r))
Simplify each term:
-
First term: r(r23r−rr)=r(r3−1)=3−r
-
Second term: −2012(r211r2−r2)=−2012(11−r2)=−2012×11+2012r2=−22132+2012r2
-
Third term: 2013(r11r2−3r2)=2013(11r−3r2)=2013×11r−2013×3r2=22143r−6039r2
Now, combine these terms to get Dr: Dr=(3−r)+(−22132+2012r2)+(22143r−6039r2)
Group terms by powers of r: Dr=(2012r2−6039r2)+(−r+22143r)+(3−22132) Dr=(2012−6039)r2+(−1+22143)r+(3−22132) Dr=−4027r2+22142r−22129
Next, we need to calculate the sum ∑r=15Dr: ∑r=15Dr=∑r=15(−4027r2+22142r−22129) This can be written as: ∑r=15Dr=−4027∑r=15r2+22142∑r=15r−22129∑r=151
We use the sum formulas for powers of natural numbers: ∑r=1nr=2n(n+1) ∑r=1nr2=6n(n+1)(2n+1)
For n=5: ∑r=15r=25(5+1)=25×6=15 ∑r=15r2=65(5+1)(2×5+1)=65×6×11=55 ∑r=151=5
Substitute these values into the sum expression: ∑r=15Dr=−4027(55)+22142(15)−22129(5)
Calculate the products: −4027×55=−221485 22142×15=332130 −22129×5=−110645
Now, sum these values: ∑r=15Dr=−221485+332130−110645 ∑r=15Dr=332130−(221485+110645) ∑r=15Dr=332130−332130 ∑r=15Dr=0
The final answer is 0.
