Question

Consider a point A far away from short dipole p. By keeping r constant, $\theta$ varies from 0° to 360°. Variation of potential of dipole at A with respect to $\theta$:-

• A. Graph (1)
• B. Graph (2)
• C. Graph (3)
• D. Graph (4)

Answer 1

Answer: (A)

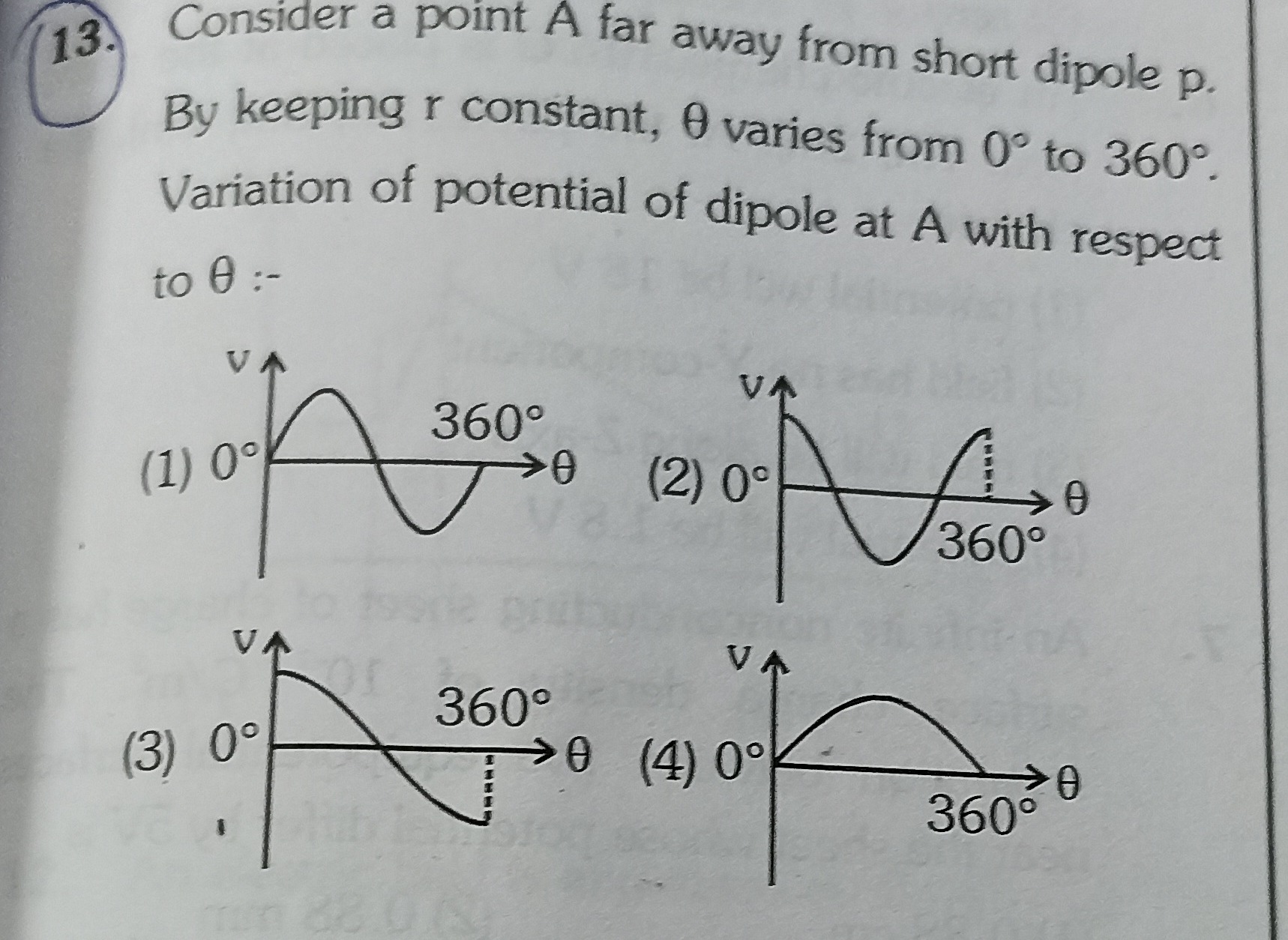
Graph (1) correctly represents the variation of potential of a dipole with respect to $\theta$.

Answer 2

The electric potential $V$ at a point $(r, \theta)$ due to a short electric dipole of dipole moment $\vec{p}$ is given by the formula:

$V = \frac{1}{4\pi\epsilon_0} \frac{p \cos\theta}{r^2}$

In this problem, the point A is far away from the dipole, so the short dipole approximation is valid. We are given that $r$ is constant, and $\theta$ varies from 0° to 360°.

Since $p$, $r$, and $\frac{1}{4\pi\epsilon_0}$ are constants, the potential $V$ is directly proportional to $\cos\theta$.

$V \propto \cos\theta$

Let's analyze the behavior of $\cos\theta$ as $\theta$ varies from 0° to 360°:

• At $\theta = 0^\circ$: $\cos(0^\circ) = 1$. So, $V$ will be maximum positive.
• At $\theta = 90^\circ$: $\cos(90^\circ) = 0$. So, $V$ will be zero.
• At $\theta = 180^\circ$: $\cos(180^\circ) = -1$. So, $V$ will be maximum negative.
• At $\theta = 270^\circ$: $\cos(270^\circ) = 0$. So, $V$ will be zero.
• At $\theta = 360^\circ$: $\cos(360^\circ) = 1$. So, $V$ will be maximum positive (same as at 0°).

Therefore, Graph (1) correctly represents the variation of potential of a dipole with respect to $\theta$.