Question

Calculate $\Delta G^{\circ}$ for the following cell reaction

$Zn(s) + Ag_2O(s) + H_2O(l) \rightarrow Zn^{2+}(aq) + 2Ag(s) + 2OH^-(aq)$

$E_{Ag^+/Ag}^0 = +0.80V$ and $E_{Zn^{+2}/Zn}^0 = -0.76V, F = 96500$

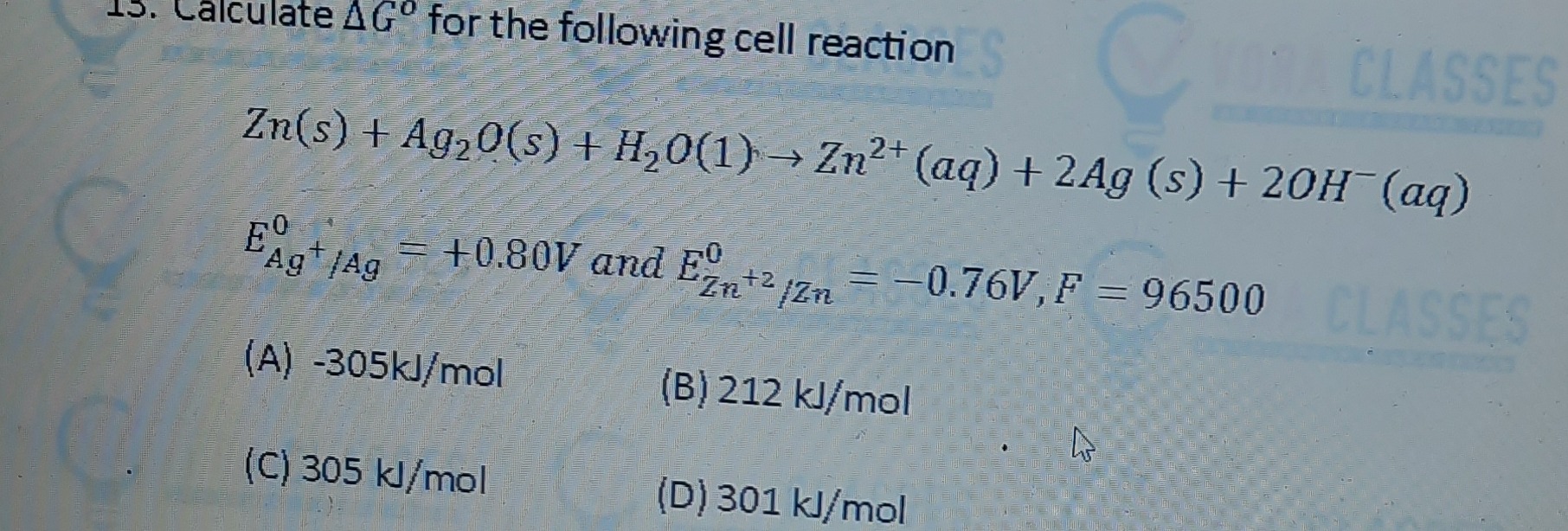
• A. -305kJ/mol
• B. 212 kJ/mol
• C. 305 kJ/mol
• D. 301 kJ/mol

Answer 1

Answer: (A)

-305kJ/mol

Answer 2

To calculate $\Delta G^{\circ}$, we use the formula:

$\Delta G^{\circ} = -nFE_{cell}^{\circ}$

First, we need to identify the half-reactions and the number of electrons ($n$) transferred.

1. Oxidation half-reaction (Anode):

$Zn(s) \rightarrow Zn^{2+}(aq) + 2e^-$

2. Reduction half-reaction (Cathode):

$Ag_2O(s) + H_2O(l) + 2e^- \rightarrow 2Ag(s) + 2OH^-(aq)$

From the balanced half-reactions, it is clear that $n=2$ electrons are transferred in the overall reaction.

Next, we calculate the standard cell potential ($E_{cell}^{\circ}$). The standard electrode potentials given are:

$E_{Ag^+/Ag}^0 = +0.80V$ (Standard reduction potential for the cathode)

$E_{Zn^{2+}/Zn}^0 = -0.76V$ (Standard reduction potential for the anode)

The standard cell potential is calculated as:

$E_{cell}^{\circ} = E_{cathode}^{\circ} - E_{anode}^{\circ}$

$E_{cell}^{\circ} = E_{Ag^+/Ag}^0 - E_{Zn^{2+}/Zn}^0$

$E_{cell}^{\circ} = (+0.80V) - (-0.76V)$

$E_{cell}^{\circ} = 0.80V + 0.76V$

$E_{cell}^{\circ} = 1.56V$

Now, substitute the values of $n$, $F$, and $E_{cell}^{\circ}$ into the $\Delta G^{\circ}$ formula: Given Faraday constant $F = 96500$ C/mol.

$\Delta G^{\circ} = -(2 \text{ mol})(96500 \text{ C/mol})(1.56 \text{ V})$

$\Delta G^{\circ} = -301080 \text{ J}$

To express $\Delta G^{\circ}$ in kilojoules (kJ), divide by 1000:

$\Delta G^{\circ} = -301.08 \text{ kJ/mol}$

Our calculated value is -301.08 kJ/mol. Option (A) is -305 kJ/mol. While not an exact match, it is the only option with the correct sign and is numerically the closest among the negative options.