Question
Question: AD and BE are the medians of a triangle ABC. If AD = 4, $\angle DAB=\frac{\pi}{6}$, $\angle ABE=\fra...
AD and BE are the medians of a triangle ABC. If AD = 4, ∠DAB=6π, ∠ABE=3π, then area of triangle ABC equals
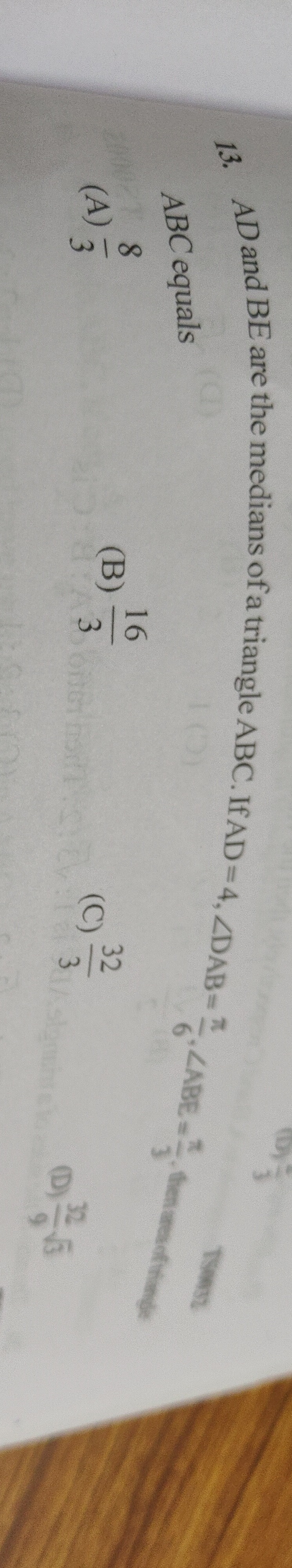
38
316
332
9323
9323
Solution
Let G be the centroid of triangle ABC, which is the intersection point of the medians AD and BE.
-
Properties of the Centroid: The centroid divides each median in the ratio 2:1. Given AD = 4, we have AG = (2/3)AD = (2/3) * 4 = 8/3.
-
Analyze Triangle ABG: We are given the angles: ∠DAB=6π. This is ∠GAB. ∠ABE=3π. This is ∠GBA. The sum of these two angles in triangle ABG is: ∠GAB+∠GBA=6π+3π=6(π+2π)=63π=2π. Since the sum of two angles in ΔABG is 2π, the third angle must be: ∠AGB=π−(∠GAB+∠GBA)=π−2π=2π. Thus, triangle ABG is a right-angled triangle with the right angle at G.
-
Calculate side AB: In the right-angled triangle ABG, we know AG = 8/3 and ∠GBA=3π. We can use the sine function: sin(∠GBA) = AG / AB sin(3π) = (8/3) / AB 23 = (8/3) / AB AB = (8/3) * (32) = 3316.
-
Calculate Area of Triangle ABD: Since AD is a median, it divides triangle ABC into two triangles of equal area: ΔABD and ΔACD. Therefore, Area(ΔABC) = 2 * Area(ΔABD). The area of ΔABD can be calculated using the formula: Area = (1/2) * product of two sides * sine of the included angle. Area(ΔABD) = (1/2) * AB * AD * sin(∠DAB) Substitute the known values: AB = 3316, AD = 4, and ∠DAB=6π. Area(ΔABD) = (1/2) * (3316) * 4 * sin(6π) Area(ΔABD) = (1/2) * (3316) * 4 * (1/2) Area(ΔABD) = (1/2) * (3316) * 2 Area(ΔABD) = 3316.
-
Calculate Area of Triangle ABC: Area(ΔABC) = 2 * Area(ΔABD) Area(ΔABC) = 2 * (3316) Area(ΔABC) = 3332.
-
Rationalize the Denominator: To rationalize the denominator, multiply the numerator and denominator by 3: Area(ΔABC) = (3332) * (33) Area(ΔABC) = 3∗3323 Area(ΔABC) = 9323.
