Question

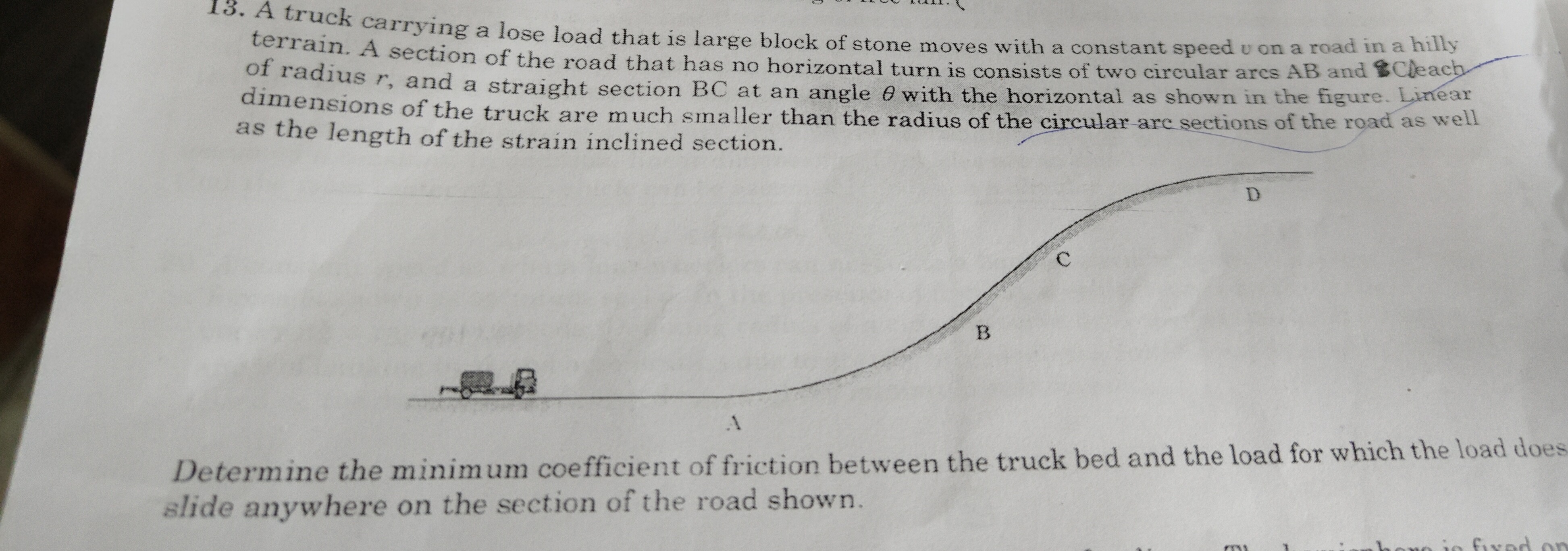
A truck carrying a lose load that is large block of stone moves with a constant speed $v$ on a road in a hilly terrain. A section of the road that has no horizontal turn is consists of two circular arcs AB and each of radius $r$, and a straight section BC at an angle $\theta$ with the horizontal as shown in the figure. Linear dimensions of the truck are much smaller than the radius of the circular arc sections of the road as well as the length of the strain inclined section.

Determine the minimum coefficient of friction between the truck bed and the load for which the load does slide anywhere on the section of the road shown.

Answer 1

$\frac{g \sin \theta}{g \cos \theta - v^2/r}$

Answer 2

The problem requires finding the minimum coefficient of static friction to prevent the load from sliding. This means we need to find the point on the path where the tendency to slide is highest, i.e., where the ratio of the required tangential force (to prevent sliding) to the normal force is maximum. We analyze three sections of the road:

1. Concave Upward Arc (AB): The normal force is $N = mg \cos \phi + mv^2/r$. The tangential force is $f_t = mg \sin \phi$. The required friction coefficient is $\mu = \frac{mg \sin \phi}{mg \cos \phi + mv^2/r}$. This is maximized at the steepest point of the arc, where $\phi = \theta$.

2. Concave Downward Arc (CD): The normal force is $N = mg \cos \phi - mv^2/r$. The tangential force is $f_t = mg \sin \phi$. The required friction coefficient is $\mu = \frac{mg \sin \phi}{mg \cos \phi - mv^2/r}$. This is maximized when the denominator is minimized, which occurs at the steepest point of the arc, where $\phi = \theta$.

3. Straight Incline (BC): The normal force is $N = mg \cos \theta$. The tangential force is $f_t = mg \sin \theta$. The required friction coefficient is $\mu = \frac{mg \sin \theta}{mg \cos \theta} = \tan \theta$.

Comparing the three expressions for the minimum required friction coefficient: $\mu_1 = \frac{g \sin \theta}{g \cos \theta + v^2/r}$ $\mu_2 = \frac{g \sin \theta}{g \cos \theta - v^2/r}$ $\mu_3 = \frac{g \sin \theta}{g \cos \theta}$

Since the numerator $g \sin \theta$ is positive, the maximum value of $\mu$ will occur when the denominator is the smallest positive value. Comparing the denominators ($g \cos \theta + v^2/r$), ($g \cos \theta - v^2/r$), and ($g \cos \theta$), the smallest positive denominator is ($g \cos \theta - v^2/r$).

Therefore, the maximum required coefficient of friction, and thus the minimum coefficient of friction for the load not to slide anywhere, is $\frac{g \sin \theta}{g \cos \theta - v^2/r}$.