Question

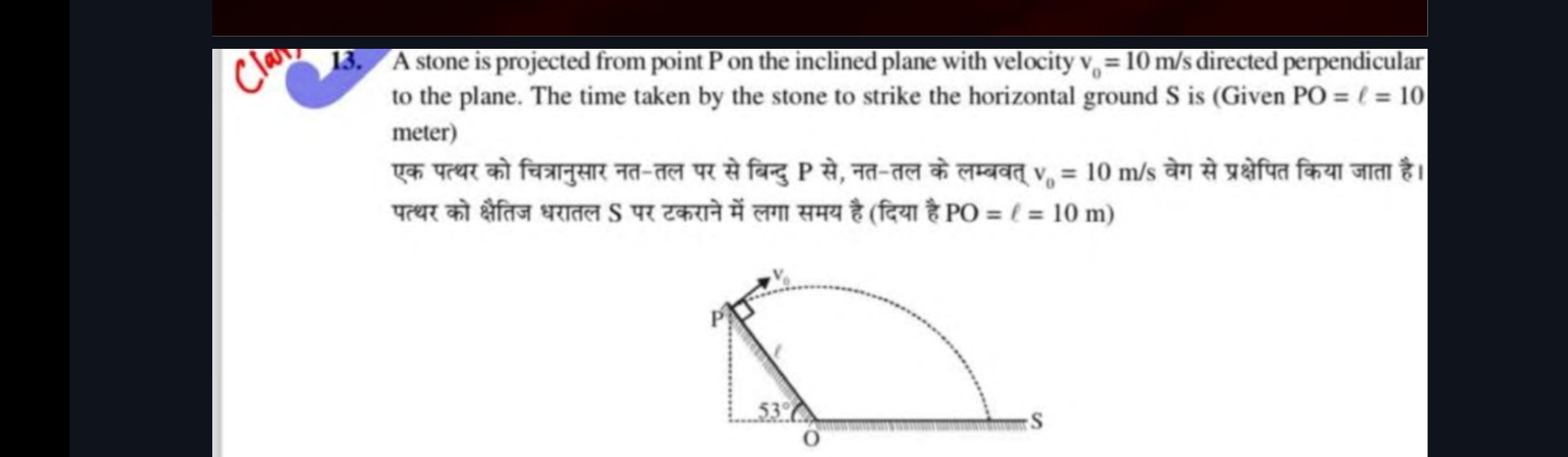
A stone is projected from point P on the inclined plane with velocity $v_0$ = 10 m/s directed perpendicular to the plane. The time taken by the stone to strike the horizontal ground S is (Given PO = $l$ = 10 meter)

Answer 1

2 s

Answer 2

The problem asks for the time taken for a stone, projected from point P on an inclined plane, to strike the horizontal ground S.

1. Determine the initial position of the stone (Point P): The inclined plane makes an angle of 53° with the horizontal. The length PO = $l = 10$ m. Let's set up a coordinate system with the origin O at the base of the inclined plane, the x-axis along the horizontal ground, and the y-axis vertically upwards. The height of point P above the horizontal ground is $y_0 = l \sin(53^\circ)$. The horizontal distance of point P from O is $x_0 = l \cos(53^\circ)$. Using the approximate values for trigonometric functions of 37° and 53° (based on a 3-4-5 right triangle): $\sin(53^\circ) = 4/5 = 0.8$ $\cos(53^\circ) = 3/5 = 0.6$ So, the initial y-coordinate of the stone is: $y_0 = 10 \times 0.8 = 8$ m.

2. Determine the initial velocity components: The initial velocity $v_0 = 10$ m/s is directed perpendicular to the inclined plane. Since the inclined plane makes an angle of 53° with the horizontal, a line perpendicular to it will make an angle of $90^\circ - 53^\circ = 37^\circ$ with the horizontal. From the diagram, the velocity vector is directed upwards and away from the plane, meaning it makes an angle of 37° above the horizontal. Let $\alpha = 37^\circ$ be the angle of projection with the horizontal. The initial velocity components are: $v_{0x} = v_0 \cos(\alpha) = 10 \cos(37^\circ)$ $v_{0y} = v_0 \sin(\alpha) = 10 \sin(37^\circ)$ Using the approximate values: $\cos(37^\circ) = 4/5 = 0.8$ $\sin(37^\circ) = 3/5 = 0.6$ So, $v_{0x} = 10 \times 0.8 = 8$ m/s. And $v_{0y} = 10 \times 0.6 = 6$ m/s.

3. Apply kinematic equations for vertical motion: The acceleration due to gravity acts downwards, so $a_y = -g$. We assume $g = 10$ m/s$^2$. $a_y = -10$ m/s$^2$. The stone strikes the horizontal ground S, which means its final y-coordinate is $y = 0$. We use the kinematic equation for vertical displacement: $y = y_0 + v_{0y}t + \frac{1}{2}a_y t^2$ Substitute the known values: $0 = 8 + (6)t + \frac{1}{2}(-10)t^2$ $0 = 8 + 6t - 5t^2$ Rearrange the equation into a standard quadratic form: $5t^2 - 6t - 8 = 0$

4. Solve the quadratic equation for time (t): Using the quadratic formula $t = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$: Here, $a=5$, $b=-6$, $c=-8$. $t = \frac{-(-6) \pm \sqrt{(-6)^2 - 4(5)(-8)}}{2(5)}$ $t = \frac{6 \pm \sqrt{36 + 160}}{10}$ $t = \frac{6 \pm \sqrt{196}}{10}$ $t = \frac{6 \pm 14}{10}$ Two possible values for $t$: $t_1 = \frac{6 + 14}{10} = \frac{20}{10} = 2$ s $t_2 = \frac{6 - 14}{10} = \frac{-8}{10} = -0.8$ s Since time cannot be negative, we take the positive value.

Therefore, the time taken by the stone to strike the horizontal ground S is 2 seconds.