Question

${12}_{c_0} \cdot {12}_{c_{10}} - {12}_{c_1} \cdot {12}_{c_9} + {12}_{c_2} \cdot {12}_{c_8} - {12}_{c_3} \cdot {12}_{c_7} \dots {12}_{c_{10}} \cdot {12}_{c_0} = -({n}_{c_r})$

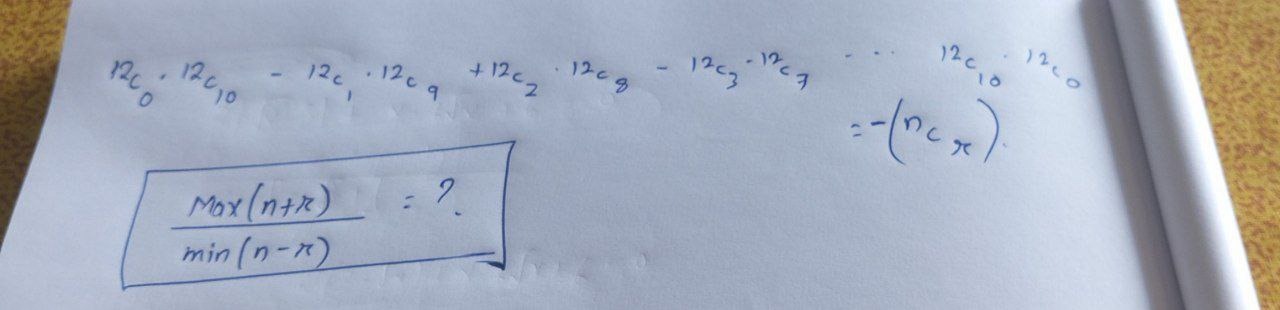
Answer 1

The expression is equal to $-{^{12}C_5}$. Thus, ${n}_{c_r} = {^{12}C_5}$, which implies $n=12$ and $r=5$.

Answer 2

The given sum is $S = \sum_{k=0}^{10} (-1)^k \cdot {^{12}C_k} \cdot {^{12}C_{10-k}}$. This sum represents the coefficient of $x^{10}$ in the expansion of $(1+x)^{12}(1-x)^{12}$. $(1+x)^{12}(1-x)^{12} = ((1+x)(1-x))^{12} = (1-x^2)^{12}$. The binomial expansion of $(1-x^2)^{12}$ is $\sum_{j=0}^{12} {^{12}C_j} (-x^2)^j = \sum_{j=0}^{12} {^{12}C_j} (-1)^j x^{2j}$. To find the coefficient of $x^{10}$, we set $2j=10$, which gives $j=5$. The coefficient is ${^{12}C_5}(-1)^5 = -{^{12}C_5}$. Therefore, the given expression is equal to $-{^{12}C_5}$. Equating this to $-({n}_{c_r})$, we have ${n}_{c_r} = {^{12}C_5}$. From this, we can conclude that $n=12$ and $r=5$.