Question
Question: If $|z|=1$ and $w = \frac{z}{z+1}$ where $z \ne -1$, then Re(w) is...
If ∣z∣=1 and w=z+1z where z=−1, then Re(w) is
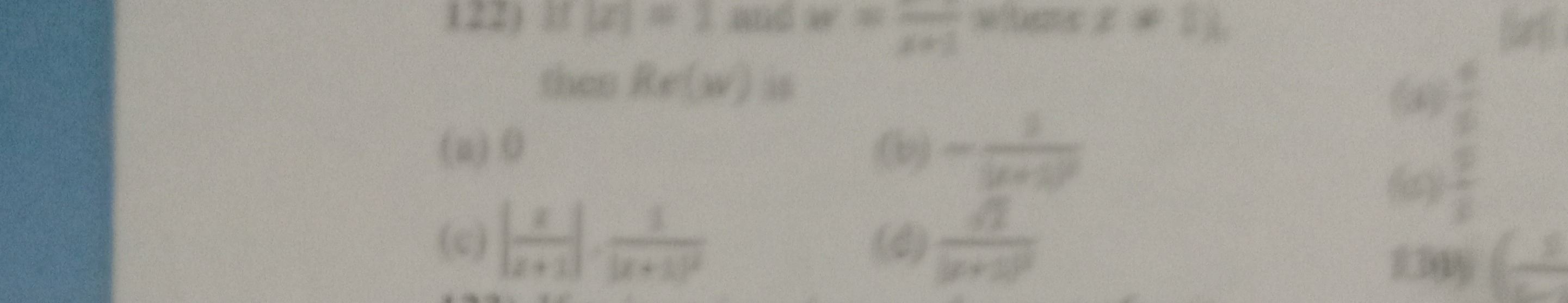
A
0
B
−2+∣z+1∣21
C
∣z+1z∣∣z+1∣21
D
∣z+1∣22
Answer
21
Explanation
Solution
Let z=eiθ (since ∣z∣=1). Then
z+1=eiθ+1=2cos2θeiθ/2.Thus,
w=z+1z=2cos2θeiθ/2eiθ=2cos2θeiθ/2.Taking the real part,
ℜ(w)=2cos2θcos2θ=21.None of the provided options match this result.
