Question
Question: Two parallel chords are drawn on the same side of the centre of a circle of radius R. It is found th...
Two parallel chords are drawn on the same side of the centre of a circle of radius R. It is found that they subtend an angle of θ and 2θ at the centre of the circle. The perpendicular distance between the chords is
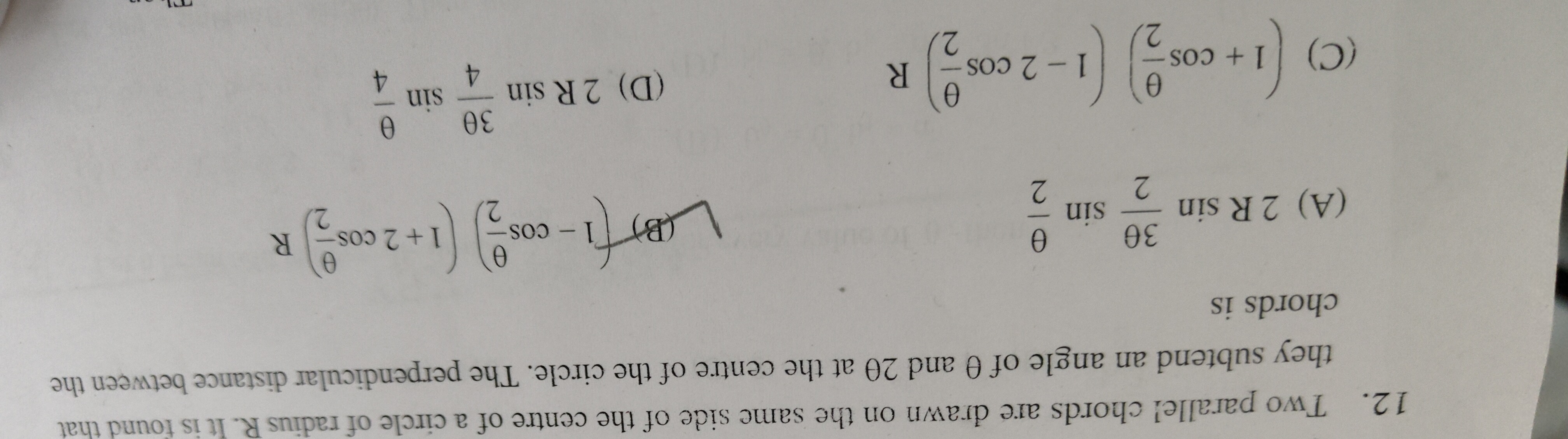
2Rsin23θsin2θ
(1−cos2θ)(1+2cos2θ)R
(1+cos2θ)(1−2cos2θ)R
2Rsin43θsin4θ
B, D
Solution
To find the perpendicular distance between the two parallel chords, we first determine their individual distances from the center of the circle.
Let the radius of the circle be R and its center be O. Let the two parallel chords be AB and CD. Since they are on the same side of the center, the longer chord will be closer to the center. The length of a chord is given by 2Rsin(α/2), where α is the angle subtended by the chord at the center. The distance of a chord from the center is given by Rcos(α/2).
Let chord AB subtend an angle θ at the center, so ∠AOB=θ. Let chord CD subtend an angle 2θ at the center, so ∠COD=2θ.
The distance of chord AB from the center, let's call it dAB, is:
dAB=Rcos(θ/2)
The distance of chord CD from the center, let's call it dCD, is:
dCD=Rcos(2θ/2)=Rcos(θ)
Since θ is an angle subtended by a chord, we assume θ∈(0,π). For θ∈(0,π), we have θ/2∈(0,π/2). In this interval, θ/2<θ, and the cosine function is decreasing. Therefore, cos(θ/2)>cos(θ). This implies dAB>dCD. So, chord AB is further from the center than chord CD.
The perpendicular distance between the two chords is the difference between their distances from the center, as they are on the same side:
Distance =dAB−dCD Distance =Rcos(θ/2)−Rcos(θ) Distance =R(cos(θ/2)−cos(θ))
Now, we need to compare this expression with the given options using trigonometric identities.
Option (B): (1−cos2θ)(1+2cos2θ)R
Let's expand this expression:
R(1⋅1+1⋅2cos(θ/2)−cos(θ/2)⋅1−cos(θ/2)⋅2cos(θ/2)) =R(1+2cos(θ/2)−cos(θ/2)−2cos2(θ/2)) =R(1+cos(θ/2)−2cos2(θ/2))
We know the double angle identity for cosine: cos(2x)=2cos2(x)−1. So, cos(θ)=2cos2(θ/2)−1. This implies 2cos2(θ/2)=cos(θ)+1. Substitute this into the expression:
=R(1+cos(θ/2)−(cos(θ)+1)) =R(1+cos(θ/2)−cos(θ)−1) =R(cos(θ/2)−cos(θ))
Thus, Option (B) is correct.
Option (D): 2Rsin43θsin4θ
We use the product-to-sum trigonometric identity: 2sinAsinB=cos(A−B)−cos(A+B). Let A=43θ and B=4θ.
Then A−B=43θ−4θ=42θ=2θ. And A+B=43θ+4θ=44θ=θ.
So, 2Rsin43θsin4θ=R(cos(θ/2)−cos(θ)).
Thus, Option (D) is also correct.
Both options (B) and (D) are algebraically equivalent to the derived expression for the perpendicular distance between the chords.
