Question
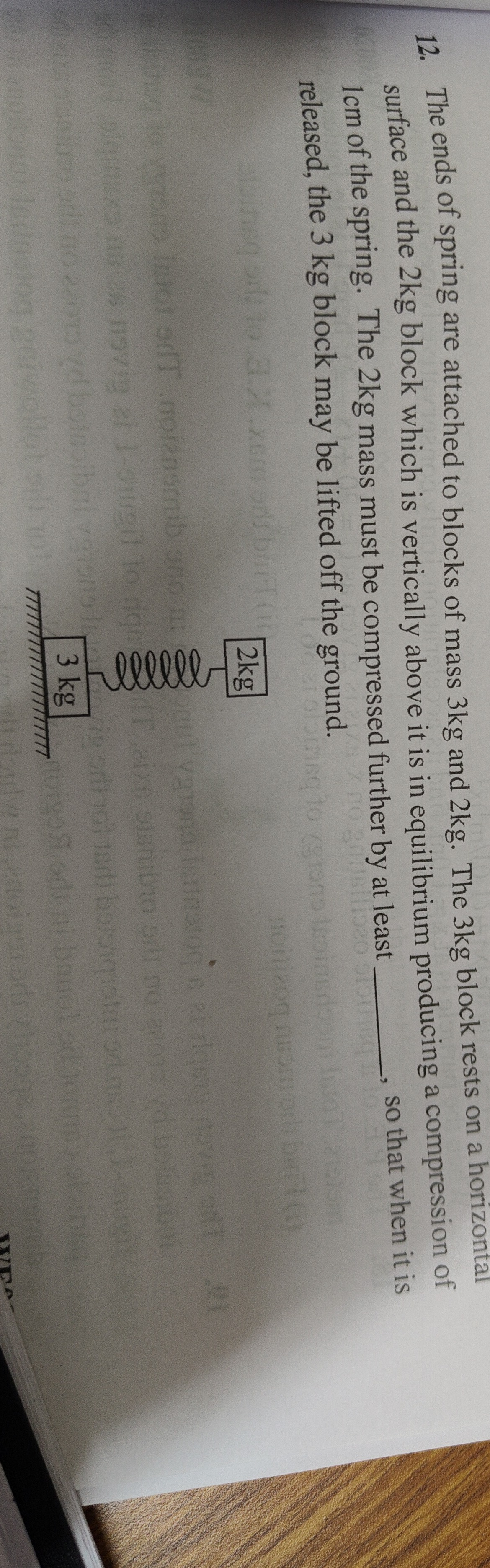
Question: The ends of spring are attached to blocks of mass 3kg and 2kg. The 3kg block rests on a horizontal s...
The ends of spring are attached to blocks of mass 3kg and 2kg. The 3kg block rests on a horizontal surface and the 2kg block which is vertically above it is in equilibrium producing a compression of 1cm of the spring. The 2kg mass must be compressed further by at least _______, so that when it is released, the 3 kg block may be lifted off the ground.
2.5 cm
Solution
The problem involves two main stages:
- Initial Equilibrium: The 2 kg block is in equilibrium, producing a compression of 1 cm (0.01 m) of the spring.
- Lift-off Condition: The 2 kg block is further compressed and then released. We need to find the minimum additional compression required for the 3 kg block to lift off the ground.
Let m1=3 kg and m2=2 kg. Let g=10 m/s2 (standard approximation, or 9.8 m/s^2, which yields the same result for 'y' as shown in thought process).
Step 1: Calculate the spring constant (k).
In the initial equilibrium state, the spring force balances the weight of the 2 kg block. Let x1=1 cm=0.01 m be the initial compression. The spring force Fs=kx1. For equilibrium of the 2 kg block: kx1=m2g k(0.01 m)=(2 kg)(10 m/s2) 0.01k=20 k=0.0120=2000 N/m
Step 2: Determine the spring extension required to lift the 3 kg block.
The 3 kg block will lift off the ground when the upward force exerted by the spring on it equals its weight. Let xextension be the extension of the spring from its natural length required for lift-off. Upward spring force Flift=kxextension. Weight of 3 kg block W1=m1g. For lift-off: Flift=W1 kxextension=m1g (2000 N/m)xextension=(3 kg)(10 m/s2) 2000xextension=30 xextension=200030=0.015 m=1.5 cm
Step 3: Apply Conservation of Energy.
Let 'y' be the additional compression of the 2 kg mass. The total initial compression from the natural length is Xinitial=x1+y=(0.01+y) meters. The 2 kg block is released from rest from this position. For the 3 kg block to be lifted, the 2 kg block must reach a position where the spring is extended by xextension=0.015 m. We consider the minimum condition, where the 2 kg block momentarily comes to rest at the lift-off position (i.e., its kinetic energy is zero at this point).
Let's set the natural length position of the spring as the reference for gravitational potential energy (h=0). Initial state (2 kg block compressed by Xinitial):
- Kinetic Energy Ki=0 (released from rest)
- Gravitational Potential Energy Ug,i=m2g(−Xinitial) (below natural length)
- Spring Potential Energy Us,i=21kXinitial2
Final state (2 kg block at lift-off position, spring extended by xextension):
- Kinetic Energy Kf=0 (minimum condition)
- Gravitational Potential Energy Ug,f=m2g(xextension) (above natural length)
- Spring Potential Energy Us,f=21kxextension2
By conservation of mechanical energy (Ki+Ug,i+Us,i=Kf+Ug,f+Us,f): 0+m2g(−Xinitial)+21kXinitial2=0+m2g(xextension)+21kxextension2 21kXinitial2−m2gXinitial=21kxextension2+m2gxextension
Substitute the known values: k=2000 N/m, m2=2 kg, g=10 m/s2, xextension=0.015 m. 21(2000)Xinitial2−(2)(10)Xinitial=21(2000)(0.015)2+(2)(10)(0.015) 1000Xinitial2−20Xinitial=1000(0.000225)+20(0.015) 1000Xinitial2−20Xinitial=0.225+0.3 1000Xinitial2−20Xinitial=0.525
Rearrange into a quadratic equation: 1000Xinitial2−20Xinitial−0.525=0
Using the quadratic formula X=2a−b±b2−4ac: a=1000, b=−20, c=−0.525 Xinitial=2(1000)−(−20)±(−20)2−4(1000)(−0.525) Xinitial=200020±400+2100 Xinitial=200020±2500 Xinitial=200020±50
Since Xinitial represents a compression, it must be positive. Xinitial=200020+50=200070=0.035 m
This Xinitial is the total compression from the natural length. We know Xinitial=x1+y. 0.035 m=0.01 m+y y=0.035 m−0.01 m y=0.025 m
Converting to centimeters: y=2.5 cm
The 2 kg mass must be compressed further by at least 2.5 cm.
The final answer is 2.5 cm.
Explanation of the solution:
- Determine spring constant (k): Use the initial equilibrium condition where the 2kg mass is balanced by the spring force, with 1cm compression. k×(0.01 m)=2 kg×g.
- Determine extension for lift-off: Calculate the spring extension required for the spring force to equal the weight of the 3kg block. k×xextension=3 kg×g.
- Apply energy conservation: Set up the energy conservation equation for the 2kg block and the spring. The initial state is the 2kg block compressed by (0.01+y) from natural length, released from rest. The final state is the 2kg block at the position where the spring is extended by xextension, with minimum kinetic energy (zero). Solve the resulting quadratic equation for the total initial compression (0.01+y), then find 'y'.
