Question
Question: The differential equation for the family of curves $y = c(x-c)^2$, where c is an arbitrary constant ...
The differential equation for the family of curves y=c(x−c)2, where c is an arbitrary constant is:
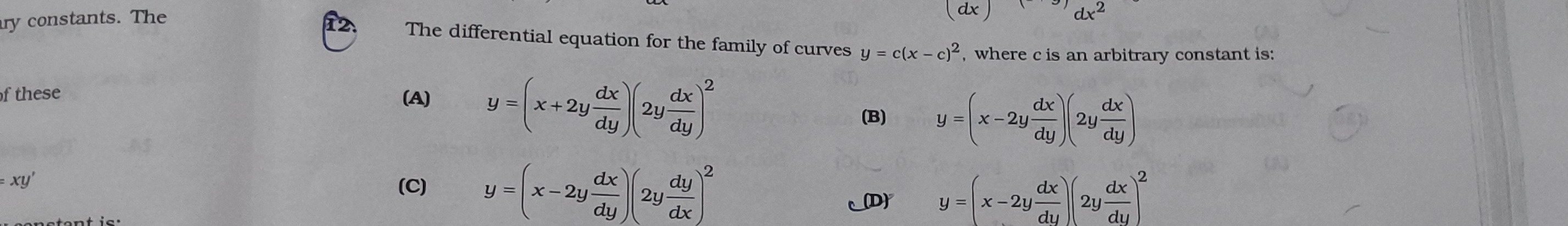
y=(x+2ydydx)(2ydydx)2
y=(x−2ydydx)(2ydydx)
y=(x−2ydydx)(2ydxdy)2
y=(x−2ydydx)(2ydydx)2
(D)
Solution
To find the differential equation for the family of curves y=c(x−c)2, we need to eliminate the arbitrary constant 'c'.
Given equation: y=c(x−c)2(1)
Differentiate equation (1) with respect to x: dxdy=dxd[c(x−c)2] Since 'c' is a constant, we use the chain rule for (x−c)2: dxdy=c⋅2(x−c)⋅dxd(x−c) dxdy=c⋅2(x−c)⋅1 dxdy=2c(x−c)(2)
Now we have two equations:
- y=c(x−c)2
- dxdy=2c(x−c)
We can eliminate 'c' and (x−c) terms. Divide equation (1) by equation (2): dxdyy=2c(x−c)c(x−c)2 dxdyy=2x−c
From this, we can express (x−c) in terms of y and dxdy: x−c=dxdy2y Since dxdy1=dydx, we can write: x−c=2ydydx(3)
Now, we need to find 'c'. From equation (3): c=x−2ydydx(4)
Substitute the expressions for 'c' from (4) and (x−c) from (3) back into the original equation (1): y=c(x−c)2 y=(x−2ydydx)(2ydydx)2
This is the differential equation for the given family of curves.
