Question

$\lim_{x\to\infty} \frac{\sqrt{x}}{\sqrt{x+\sqrt{x}}}$

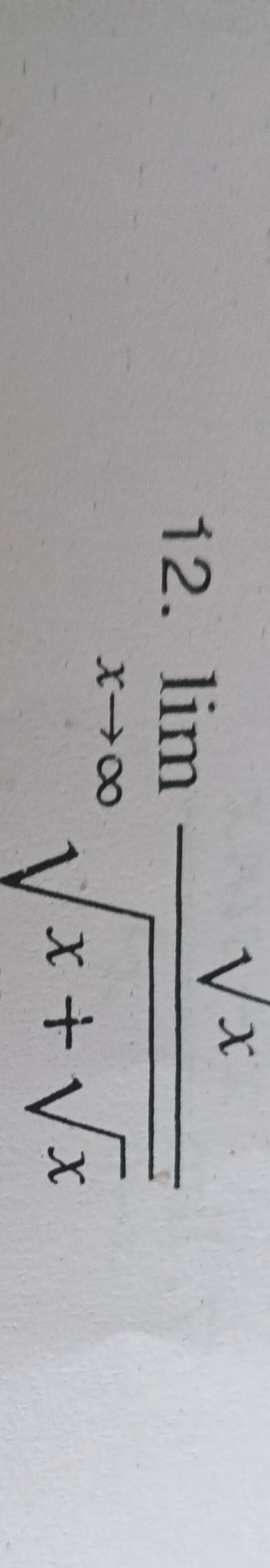
Answer 1

1

Answer 2

To evaluate the limit $\lim_{x\to\infty} \frac{\sqrt{x}}{\sqrt{x+\sqrt{x}}}$, we can divide the numerator and the denominator by $\sqrt{x}$.

The expression becomes:

$\lim_{x\to\infty} \frac{\frac{\sqrt{x}}{\sqrt{x}}}{\frac{\sqrt{x+\sqrt{x}}}{\sqrt{x}}}$

Simplify the numerator and the denominator:

Numerator: $\frac{\sqrt{x}}{\sqrt{x}} = 1$.

Denominator: $\frac{\sqrt{x+\sqrt{x}}}{\sqrt{x}} = \sqrt{\frac{x+\sqrt{x}}{x}} = \sqrt{\frac{x}{x} + \frac{\sqrt{x}}{x}} = \sqrt{1 + \frac{1}{\sqrt{x}}}$.

So the limit expression is:

$\lim_{x\to\infty} \frac{1}{\sqrt{1 + \frac{1}{\sqrt{x}}}}$

Now, we evaluate the limit as $x \to \infty$.

As $x \to \infty$, $\sqrt{x} \to \infty$.

As $\sqrt{x} \to \infty$, $\frac{1}{\sqrt{x}} \to 0$.

Therefore, the term inside the square root in the denominator approaches $1+0 = 1$.

The square root of this term approaches $\sqrt{1} = 1$.

So, the limit is:

$\frac{1}{\sqrt{1+0}} = \frac{1}{\sqrt{1}} = \frac{1}{1} = 1$