Question
Question: $\lim_{n\to\infty} \frac{\int_{1/(n+1)}^{1/n} \tan^{-1}(nx)dx}{\int_{1/(n+1)}^{1/n} \sin^{-1}(nx)dx}...
limn→∞∫1/(n+1)1/nsin−1(nx)dx∫1/(n+1)1/ntan−1(nx)dx is equal to
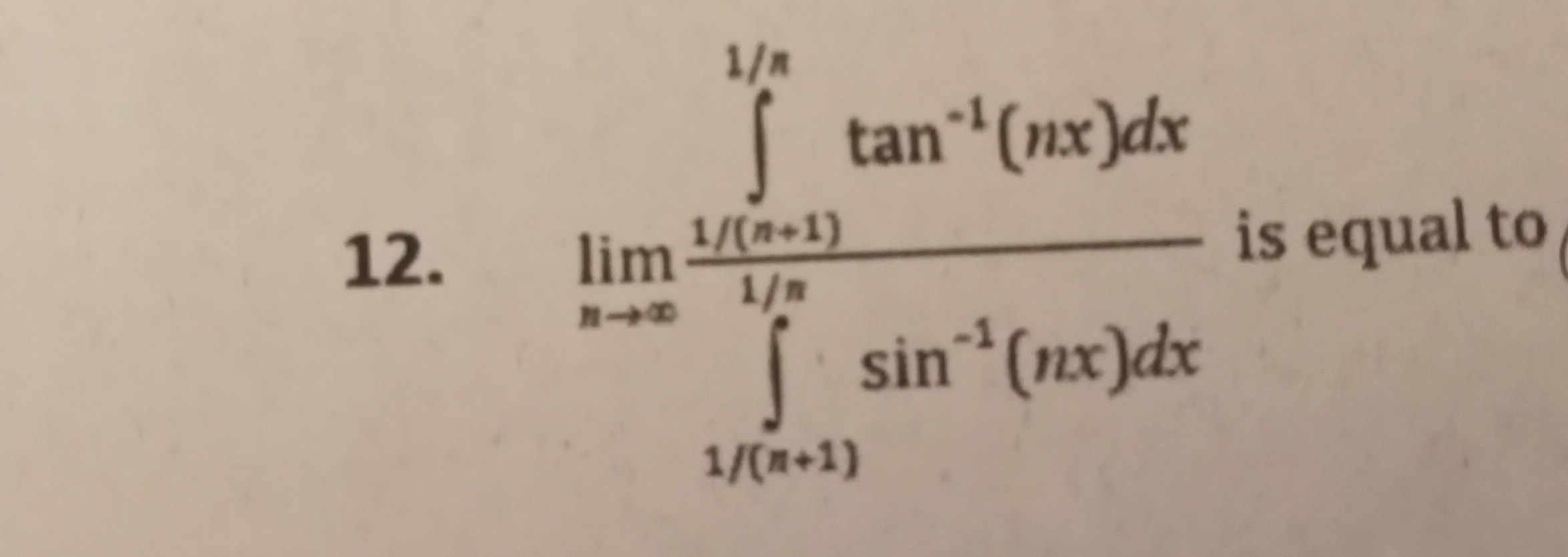
1
2
1/2
1/4
21
Solution
Let the given limit be L. L=limn→∞∫1/(n+1)1/nsin−1(nx)dx∫1/(n+1)1/ntan−1(nx)dx We use the substitution u=nx, so du=ndx, which means dx=ndu. When x=n+11, u=n+1n. When x=n1, u=1.
The integrals become: ∫1/(n+1)1/ntan−1(nx)dx=∫n/(n+1)1tan−1(u)ndu=n1∫n/(n+1)1tan−1(u)du ∫1/(n+1)1/nsin−1(nx)dx=∫n/(n+1)1sin−1(u)ndu=n1∫n/(n+1)1sin−1(u)du
The limit expression simplifies to: L=limn→∞n1∫n/(n+1)1sin−1(u)dun1∫n/(n+1)1tan−1(u)du=limn→∞∫n/(n+1)1sin−1(u)du∫n/(n+1)1tan−1(u)du Let an=n+1n. As n→∞, an→1. The limit is of the form 00. L=liman→1−∫an1sin−1(u)du∫an1tan−1(u)du Applying L'Hopital's Rule: L=liman→1−dand∫an1sin−1(u)dudand∫an1tan−1(u)du=liman→1−−sin−1(an)−tan−1(an)=liman→1−sin−1(an)tan−1(an) Substituting an=1: L=sin−1(1)tan−1(1)=π/2π/4=21
