Question
Question: Let $D_n = [a_{ij}]_{n \times n}$ be a $(n \times n)$ determinant with the following conditions $a_...
Let Dn=[aij]n×n be a (n×n) determinant with the following conditions
aij=⎩⎨⎧420i=j∣i−j∣=1otherwise
Then,
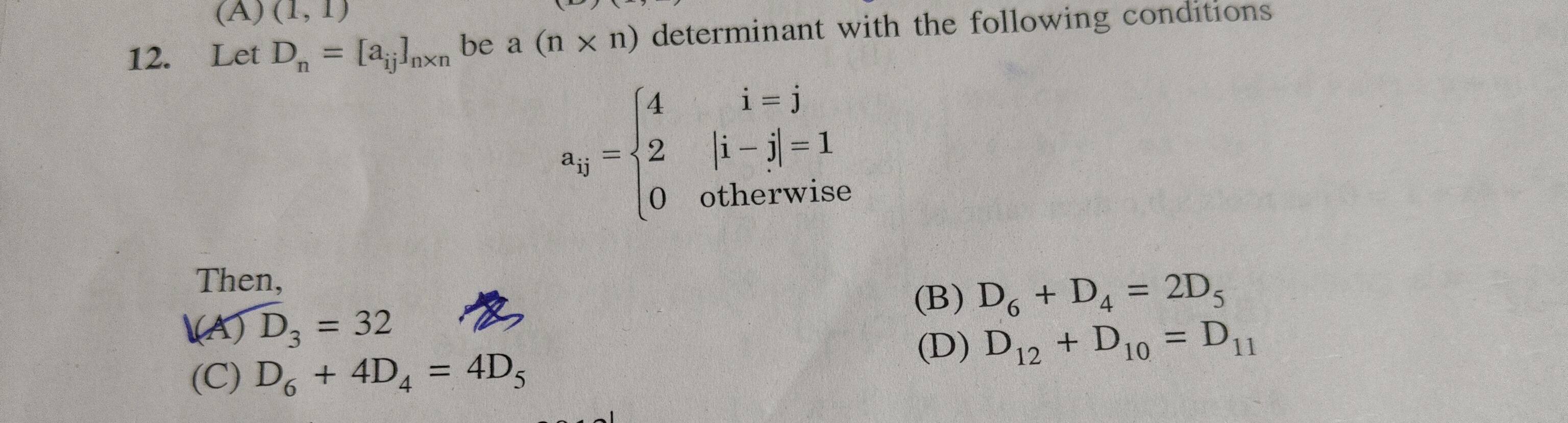
D3=32
D6+D4=2D5
D6+4D4=4D5
D12+D10=D11
A, C
Solution
Here's how to solve this problem:
-
Calculate initial determinants:
- D1=4
- D2=4224=16−4=12
- D3=420242024=4(16−4)−2(8)=48−16=32
This directly verifies option (A).
-
Derive the recurrence relation:
Expand Dn along the first row. The cofactor of a11 is Dn−1. The cofactor of a12 is −2Dn−2. This leads to the recurrence:
Dn=4Dn−1−4Dn−2
-
Verify options using the recurrence relation:
-
Option (B): D6+D4=2D5. Substitute D6=4D5−4D4. This simplifies to 4D5−4D4+D4=2D5, which further simplifies to 2D5=3D4. This is false.
-
Option (C): D6+4D4=4D5. Substitute D6=4D5−4D4. This simplifies to 4D5−4D4+4D4=4D5, which simplifies to 4D5=4D5. This is true.
-
Option (D): D12+D10=D11. Substitute D12=4D11−4D10. This simplifies to 4D11−4D10+D10=D11, which further simplifies to 3D11=3D10 or D11=D10. This is false.
-
Therefore, the correct options are (A) and (C).
