Question

If the tangent at (h,k) to the ellipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ cuts the auxiliary circle in points whose ordinates are $y_1$ and $y_2$, show that $\frac{1}{y_1}+\frac{1}{y_2}=\frac{2}{k}$.

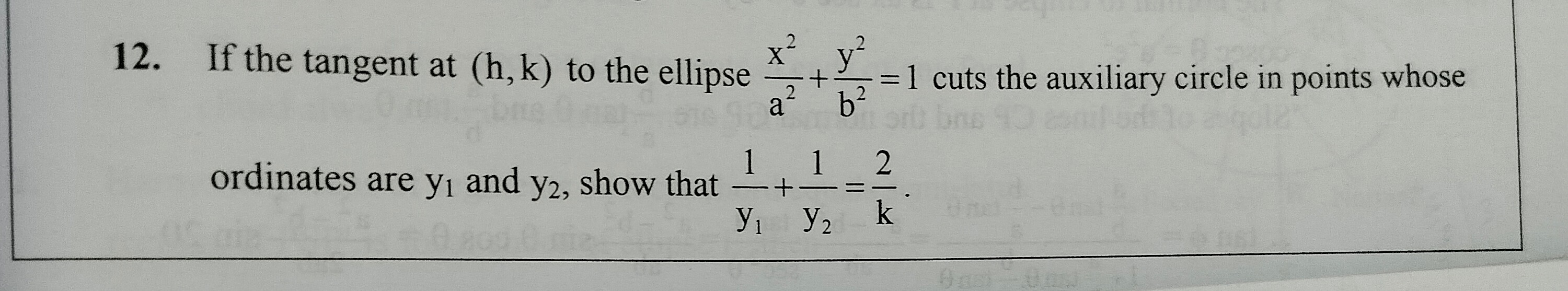
Answer 1

The relation $\frac{1}{y_1}+\frac{1}{y_2}=\frac{2}{k}$ is proven.

Answer 2

The equation of the tangent to the ellipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ at $(h,k)$ is $\frac{xh}{a^2}+\frac{yk}{b^2}=1$. The auxiliary circle is $x^2+y^2=a^2$. Solving these equations for $y$ gives a quadratic equation whose roots are $y_1$ and $y_2$. Using Vieta's formulas for the sum and product of roots, and the condition that $(h,k)$ lies on the ellipse, we can show that $\frac{1}{y_1}+\frac{1}{y_2}=\frac{2}{k}$.