Question
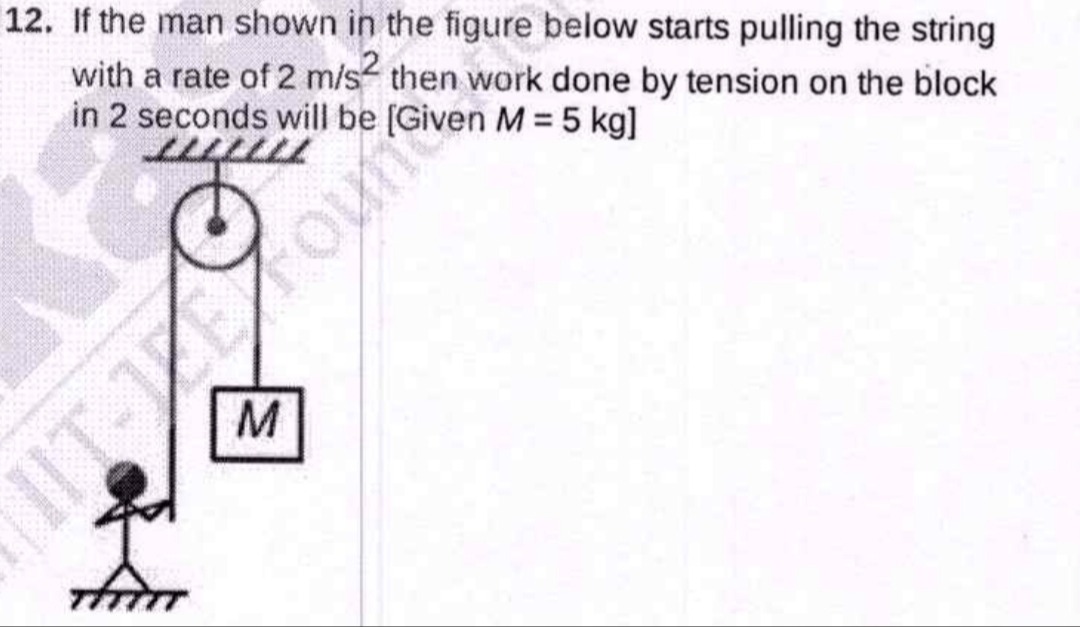
Question: If the man shown in the figure below starts pulling the string with a rate of 2 m/s² then work done ...
If the man shown in the figure below starts pulling the string with a rate of 2 m/s² then work done by tension on the block in 2 seconds will be [Given M = 5 kg]
Answer
240 J
Explanation
Solution
- Acceleration of the block: The man pulls the string with an acceleration of a=2 m/s2. Since the pulley is ideal and the string is inextensible, the block also accelerates upwards with the same acceleration a=2 m/s2.
- Tension in the string: Applying Newton's second law to the block of mass M, the net force is T−Mg. Thus, T−Mg=Ma, which gives the tension T=M(g+a). Assuming g=10 m/s2, T=5 kg×(10 m/s2+2 m/s2)=5×12=60 N.
- Displacement of the block: The block starts from rest (u=0) and accelerates at a=2 m/s2 for t=2 s. Using the kinematic equation d=ut+21at2, the displacement is d=(0)(2)+21(2)(2)2=4 m.
- Work done by tension: The work done by tension (W) is given by W=T×d, as tension and displacement are in the same direction (upwards). Therefore, W=60 N×4 m=240 J.
