Solveeit Logo
Login

Question

Question: If $(4x^2+1)^n = \sum_{r=0}^{n} a_r (1+x^2)^{n-r} x^{2r}$, then the value of $\sum_{r=0}^{n} a_r$ is...

If (4x2+1)n=∑r=0nar(1+x2)n−rx2r(4x^2+1)^n = \sum_{r=0}^{n} a_r (1+x^2)^{n-r} x^{2r}, then the value of ∑r=0nar\sum_{r=0}^{n} a_r is

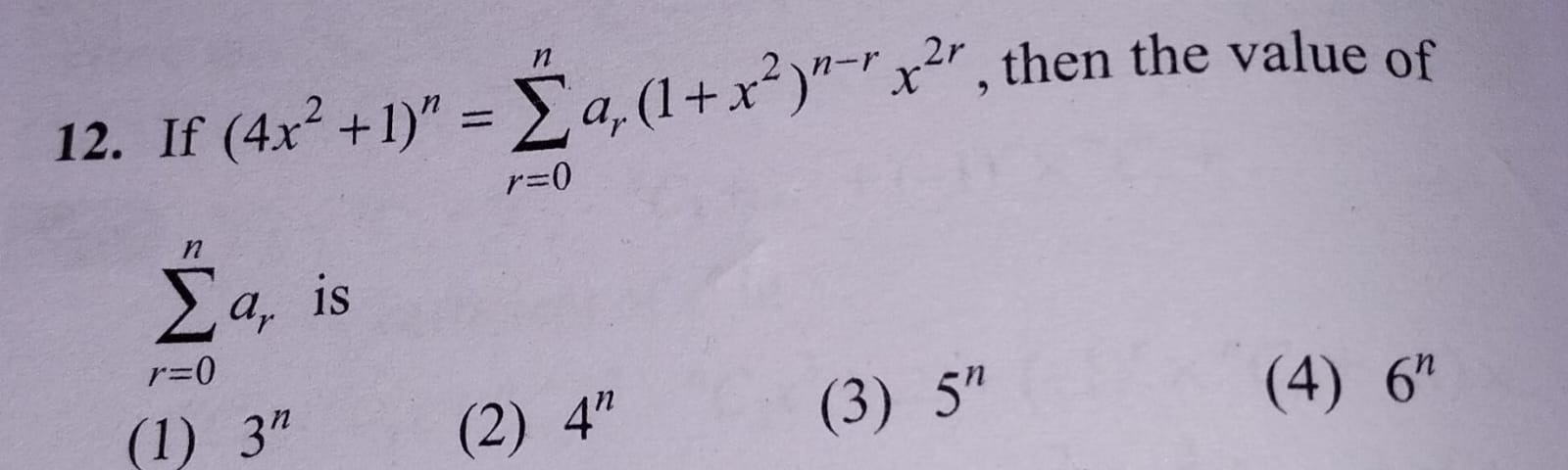
A

3n3^n

B

4n4^n

C

5n5^n

D

6n6^n

Answer

4n4^n

Explanation

Solution

The given identity is (4x2+1)n=∑r=0nar(1+x2)n−rx2r(4x^2+1)^n = \sum_{r=0}^{n} a_r (1+x^2)^{n-r} x^{2r}. We can rewrite the LHS as 4x2+1=(1+x2)+3x24x^2+1 = (1+x^2) + 3x^2. So, ((1+x2)+3x2)n=∑r=0n(nr)(1+x2)n−r(3x2)r=∑r=0n(nr)3r(1+x2)n−rx2r((1+x^2) + 3x^2)^n = \sum_{r=0}^n \binom{n}{r} (1+x^2)^{n-r} (3x^2)^r = \sum_{r=0}^n \binom{n}{r} 3^r (1+x^2)^{n-r} x^{2r}. Comparing coefficients with the given RHS, we get ar=(nr)3ra_r = \binom{n}{r} 3^r. Then, ∑r=0nar=∑r=0n(nr)3r\sum_{r=0}^{n} a_r = \sum_{r=0}^{n} \binom{n}{r} 3^r. By the binomial theorem, this sum is (1+3)n=4n(1+3)^n = 4^n.