Question

Given that the cubic $ax^3 - ax^2 + 9bx - b = 0$ ($a \neq 0$) has all three positive roots. Find the harmonic mean of the roots independent of a and b, hence deduce that the root are all equal. Find also the minimum value of (a + b) if a and b ∈ N.

Answer 1

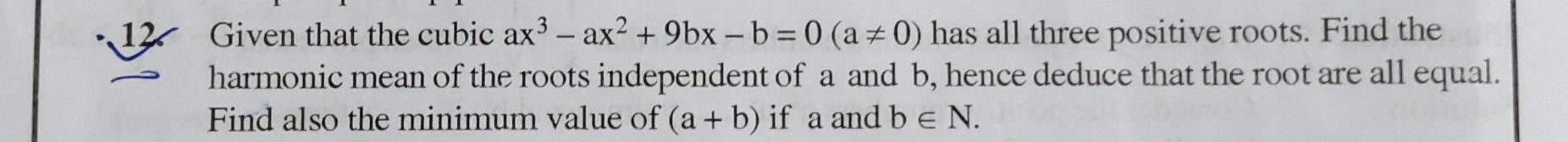
The harmonic mean of the roots is $1/3$. The roots are all equal ($\alpha = \beta = \gamma = 1/3$) because the arithmetic mean equals the harmonic mean. The minimum value of $(a + b)$ is $28$.

Answer 2

The given cubic equation is $ax^3 - ax^2 + 9bx - b = 0$ ($a \neq 0$). Let the three positive roots be $\alpha, \beta, \gamma$.

Using Vieta's formulas:

1. Sum of the roots: $\alpha + \beta + \gamma = -(-a)/a = 1$
2. Sum of the products of the roots taken two at a time: $\alpha\beta + \beta\gamma + \gamma\alpha = 9b/a$
3. Product of the roots: $\alpha\beta\gamma = -(-b)/a = b/a$

1. Find the harmonic mean of the roots independent of a and b: The harmonic mean (HM) of three numbers $\alpha, \beta, \gamma$ is given by: $HM = \frac{3}{\frac{1}{\alpha} + \frac{1}{\beta} + \frac{1}{\gamma}}$ To simplify, find a common denominator for the sum of reciprocals: $HM = \frac{3}{\frac{\alpha\beta + \beta\gamma + \gamma\alpha}{\alpha\beta\gamma}}$ $HM = \frac{3\alpha\beta\gamma}{\alpha\beta + \beta\gamma + \gamma\alpha}$ Now, substitute the expressions from Vieta's formulas: $HM = \frac{3(b/a)}{9b/a} = \frac{3}{9} = \frac{1}{3}$ The harmonic mean of the roots is $\frac{1}{3}$, which is independent of 'a' and 'b'.

2. Deduce that the roots are all equal: The arithmetic mean (AM) of the roots is: $AM = \frac{\alpha + \beta + \gamma}{3} = \frac{1}{3}$ We have found that $HM = \frac{1}{3}$. For positive numbers, the AM-HM inequality states that $AM \ge HM$. In this case, we observe that $AM = HM = \frac{1}{3}$. The equality in the AM-HM inequality holds if and only if all the numbers are equal. Therefore, $\alpha = \beta = \gamma$. Since $AM = \frac{1}{3}$, it implies that $\alpha = \beta = \gamma = \frac{1}{3}$.

3. Find the minimum value of (a + b) if a and b ∈ N: Since the roots are $\alpha = \beta = \gamma = \frac{1}{3}$, we can use Vieta's formulas to establish a relationship between 'a' and 'b'. Using the sum of products of roots taken two at a time: $\alpha\beta + \beta\gamma + \gamma\alpha = 9b/a$ $(\frac{1}{3})(\frac{1}{3}) + (\frac{1}{3})(\frac{1}{3}) + (\frac{1}{3})(\frac{1}{3}) = \frac{9b}{a}$ $\frac{1}{9} + \frac{1}{9} + \frac{1}{9} = \frac{9b}{a}$ $\frac{3}{9} = \frac{9b}{a}$ $\frac{1}{3} = \frac{9b}{a}$ Cross-multiplying gives: $a = 27b$

Alternatively, using the product of roots: $\alpha\beta\gamma = b/a$ $(\frac{1}{3})(\frac{1}{3})(\frac{1}{3}) = \frac{b}{a}$ $\frac{1}{27} = \frac{b}{a}$ $a = 27b$ Both relations yield the same condition: $a = 27b$.

We need to find the minimum value of $(a + b)$ where $a, b \in N$ (natural numbers, i.e., positive integers). Substitute $a = 27b$ into the expression $(a + b)$: $a + b = 27b + b = 28b$ Since 'b' must be a natural number, the smallest possible value for 'b' is 1. If $b=1$, then $a = 27(1) = 27$. Both $a=27$ and $b=1$ are natural numbers. The minimum value of $(a + b)$ is $28(1) = 28$.