Solveeit Logo
Login

Question

Question: For the two reactions I: A → B; II: C → D following graph is obtained. Which of the following is tr...

For the two reactions I: A → B; II: C → D following graph is obtained.

Which of the following is true:

A

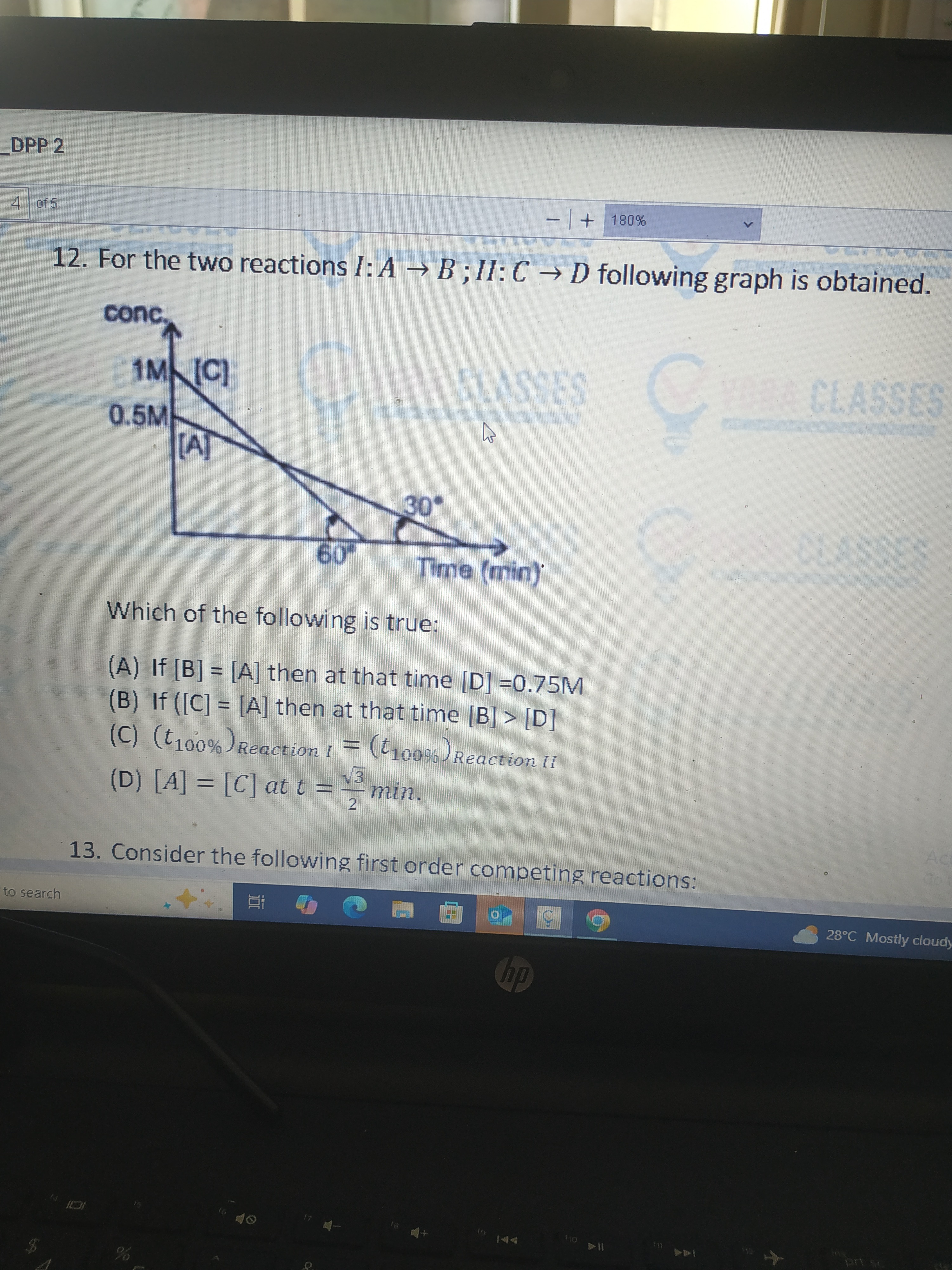
If [B] = [A] then at that time [D] =0.75M

B

If ([C] = [A] then at that time [B] > [D]

C

(t100%)ReactionI(t_{100\%})_{Reaction I} = (t100%)ReactionII(t_{100\%})_{Reaction II}

D

[A] = [C] at t = 32\frac{\sqrt{3}}{2} min.

Answer

If [B] = [A] then at that time [D] = 0.75M

Explanation

Solution

The problem describes two zero-order reactions, I: A → B and II: C → D, and provides a graph of reactant concentration versus time.

1. Determine Initial Concentrations and Rate Constants: From the graph:

  • Initial concentration of A, [A]0=0.5[A]_0 = 0.5 M.
  • Initial concentration of C, [C]0=1[C]_0 = 1 M.

For a zero-order reaction, the rate law is: Rate =k= k The integrated rate law is: [R]t=[R]0−kt[R]_t = [R]_0 - kt The slope of the concentration vs. time graph is −k-k.

The angles shown in the graph are 60° for reaction I (A) and 30° for reaction II (C).

Let's assume the angles given (60° and 30°) are with respect to the concentration (vertical) axis. This means the angles with the time (horizontal) axis would be 90∘−60∘=30∘90^\circ - 60^\circ = 30^\circ for reaction I, and 90∘−30∘=60∘90^\circ - 30^\circ = 60^\circ for reaction II. With this interpretation:

  • For reaction I: Angle with time axis = 30°. Slope = −tan⁡(30∘)=−1/3-\tan(30^\circ) = -1/\sqrt{3}. So, kI=1/3k_I = 1/\sqrt{3} M/min.
  • For reaction II: Angle with time axis = 60°. Slope = −tan⁡(60∘)=−3-\tan(60^\circ) = -\sqrt{3}. So, kII=3k_{II} = \sqrt{3} M/min.

2. Evaluate Each Option:

A) If [B] = [A] then at that time [D] = 0.75M For reaction I: A → B, [B]t=[A]0−[A]t[B]_t = [A]_0 - [A]_t. Given [B]t=[A]t[B]_t = [A]_t: [A]t=[A]0−[A]t  ⟹  2[A]t=[A]0  ⟹  [A]t=[A]0/2[A]_t = [A]_0 - [A]_t \implies 2[A]_t = [A]_0 \implies [A]_t = [A]_0/2. So, [A]t=0.5/2=0.25[A]_t = 0.5/2 = 0.25 M. Now find the time tt when [A]t=0.25[A]_t = 0.25 M: [A]t=[A]0−kIt[A]_t = [A]_0 - k_I t 0.25=0.5−(1/3)t0.25 = 0.5 - (1/\sqrt{3})t (1/3)t=0.5−0.25=0.25(1/\sqrt{3})t = 0.5 - 0.25 = 0.25 t=0.253=34t = 0.25 \sqrt{3} = \frac{\sqrt{3}}{4} min.

Now find [D] at this time t=34t = \frac{\sqrt{3}}{4} min for reaction II: C → D. [D]t=[C]0−[C]t[D]_t = [C]_0 - [C]_t. Since C → D, [D] formed = [C] reacted. [D]t=kIIt[D]_t = k_{II} t (since [D]0=0[D]_0 = 0) [D]t=3×34=34=0.75[D]_t = \sqrt{3} \times \frac{\sqrt{3}}{4} = \frac{3}{4} = 0.75 M. This matches the statement in option (A). So, option (A) is true.

Final Answer: The final answer is A\boxed{A}

Subject: Chemistry Chapter: Chemical Kinetics Topic: Zero Order Reactions, Integrated Rate Law, Graphical Representation of Reaction Kinetics