Question

For a nonnegative integer $x$, let $f(x) = |a-b|$, where $a$ is the remainder when $x$ is divided by 77 and $b$ is the remainder when $x$ is divided by 143. For how many values of $1 \le k \le 1001$ does $0 \le f(k) \le 70$?

Answer 1

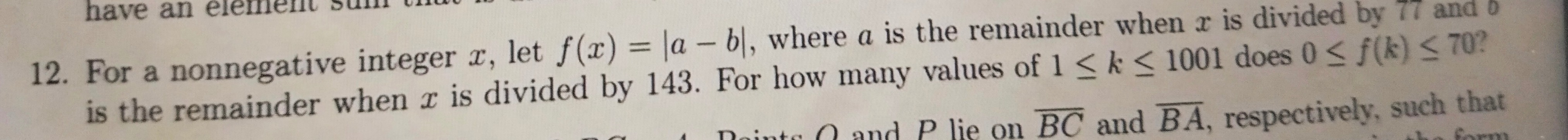
770

Answer 2

Let

$a=x \mod 77 \quad (0\le a\le76)$, $b=x \mod 143 \quad (0\le b\le142)$

Since 77 and 143 share the common factor 11, the system

$x\equiv a\pmod{77}$, $x\equiv b\pmod{143}$

has a solution if and only if

$a\equiv b\pmod{11}$.

Write $b=a+11k$, $k\in\mathbb{Z}$.

We are given $f(x)=|a-b|=|11k|=11|k|\le 70$.

Thus $|k|\le \frac{70}{11}\quad\Longrightarrow\quad |k|\le6$.

So $k\in\{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6\}$.

For the solution to be valid, besides $0\le a \le 76$, we require $0\le a+11k\le142$.

For each fixed $k$, the valid $a$ satisfy

$a\in \Bigl[\max(0,-11k),\min(76,142-11k)\Bigr]$.

Now count the number of integers $a$ for each $k$:

• For $k=-6$:

  $\max(0,66)=66$ and $\min(76,142+66=208)=76$.
  Count = $76-66+1=11$.

• For $k=-5$:

  Lower bound = $\max(0,55)=55$; upper bound = $\min(76,142+55=197)=76$.
  Count = $76-55+1=22$.

• For $k=-4$:

  Lower bound = $44$; upper bound = $76$.
  Count = $76-44+1=33$.

• For $k=-3$:

  Lower bound = $33$; upper bound = $76$.
  Count = $76-33+1=44$.

• For $k=-2$:

  Lower bound = $22$; upper bound = $76$.
  Count = $76-22+1=55$.

• For $k=-1$:

  Lower bound = $11$; upper bound = $76$.
  Count = $76-11+1=66$.

• For $k=0$:

  Lower bound = $0$; upper bound = $\min(76,142)=76$.
  Count = $76-0+1=77$.

• For $k=1,\ 2,\ 3,\ 4,\ 5,\ 6$:

  For $k\ge1$, note that $-11k\le0$ so lower bound = $0$.
  Upper bound = $142-11k$. For $k=1$ to $6$, we have:

  $142-11\ge131,\ 142-22\ge120,\ 142-33\ge109,\ 142-44\ge98,\ 142-55\ge87,\ 142-66=76$.

  In each case the upper bound is at least 76, so $a$ runs from 0 to 76.
  Count for each = $76-0+1=77$.

Now summing counts:

• Sum for $k=-6$ to $-1$: $11+22+33+44+55+66 = 231.$
• For $k=0$: $77$.
• For $k=1$ to $6$: $6\times77=462.$

Total number of solutions:

$231+77+462=770$.

Since $x$ runs modulo $\text{lcm}(77,143)=1001$, every residue in $\{0,1,2,\ldots,1000\}$ is reached exactly once. Thus, there are 770 values of $1\le k\le1001$ for which $0\le f(k)\le70$.