Question
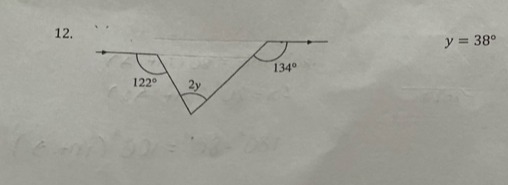
Question: 12. $y=38^\circ$...
y=38∘
The statement y=38∘ is correct.
Solution
The problem presents a geometric figure with two parallel lines and two transversals. We are given three angles: 122∘, 2y, and 134∘. The question asks to verify if y=38∘ is consistent with the given angles.
Let's label the points in the diagram to clarify the setup.
Let the top parallel line be L1 and the bottom parallel line be L2.
Let the left point where the transversal meets L1 be A.
Let the right point where the transversal meets L1 be C.
Let the common vertex where the angle 2y is located be B.
So, the figure forms a triangle ABC, where the base AC lies on the line L1, and the vertex B lies on the line L2.
Now, let's determine the interior angles of triangle ABC:
-
Angle at A: The angle given at point A is 122∘. This is an exterior angle formed by the line L1 and the segment AB. The interior angle ∠BAC of the triangle is supplementary to this exterior angle.
∠BAC=180∘−122∘=58∘. -
Angle at C: The angle given at point C is 134∘. This is an exterior angle formed by the line L1 and the segment BC. The interior angle ∠BCA of the triangle is supplementary to this exterior angle.
∠BCA=180∘−134∘=46∘. -
Angle at B: The angle given at point B is 2y. This is the interior angle ∠ABC of the triangle.
Now, we use the property that the sum of interior angles in a triangle is 180∘:
∠BAC+∠BCA+∠ABC=180∘
Substitute the values we found:
58∘+46∘+2y=180∘
104∘+2y=180∘
Now, solve for y:
2y=180∘−104∘
2y=76∘
y=276∘
y=38∘
The calculated value of y is 38∘, which matches the value given in the question (y=38∘). Therefore, the statement is consistent with the diagram.
The final answer is y=38∘.
Explanation:
- Identify the geometric figure as a triangle with its base on one parallel line and the opposite vertex on the other parallel line.
- Calculate the interior angles of the triangle at the base using the supplementary angle property (180∘−exterior angle).
- Apply the triangle angle sum theorem (sum of interior angles is 180∘).
- Solve the resulting equation for y.
- Compare the calculated value of y with the given value.
Answer: The statement y=38∘ is correct.
