Question
Question: Electric field in a region is found to be $\vec{E} = 3y\hat{j}$ The total energy stored in electric...
Electric field in a region is found to be E=3yj^
The total energy stored in electric field inside the cube shown will be :
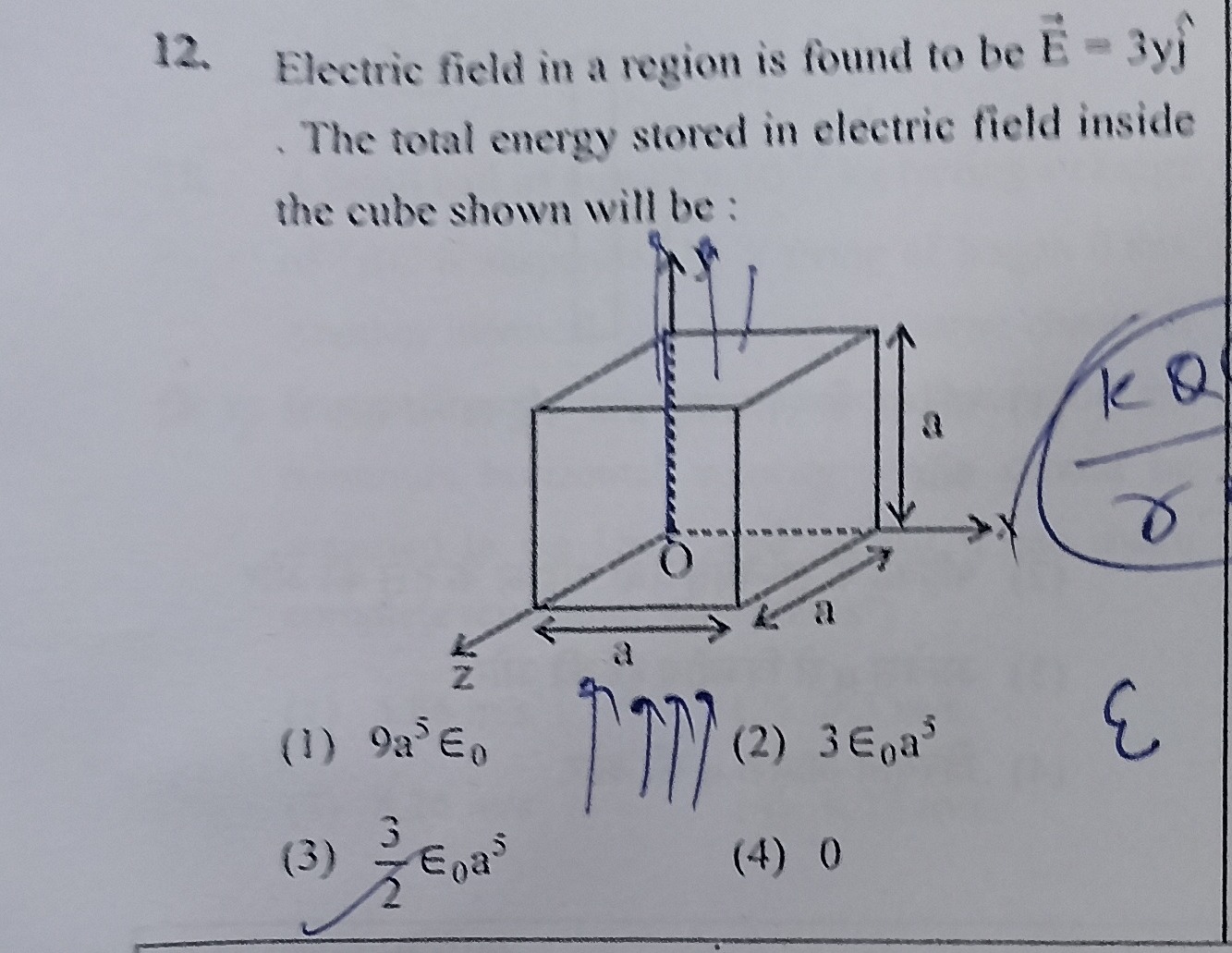
9a5ϵ0
3ϵ0a3
23ϵ0a5
0
23ϵ0a5
Solution
The total energy stored in an electric field in a given volume V is given by the integral of the energy density over that volume:
UE=∫VuEdV
where uE is the electric energy density, defined as:
uE=21ϵ0E2
Given electric field is E=3yj^. The magnitude of the electric field is E=∣E∣=∣3y∣=3y (since y is positive in the cube from 0 to a). So, E2=(3y)2=9y2.
The cube shown in the figure has side length 'a'. Assuming the origin O is at one corner, the cube extends from x=0 to x=a, y=0 to y=a, and z=0 to z=a. The volume element in Cartesian coordinates is dV=dxdydz.
Now, we can set up the integral for the total energy: UE=∫0a∫0a∫0a21ϵ0(9y2)dxdydz
We can pull out the constants from the integral: UE=29ϵ0∫0a∫0a∫0ay2dxdydz
The integral can be separated into three independent integrals: UE=29ϵ0(∫0adx)(∫0ay2dy)(∫0adz)
Evaluate each integral:
-
∫0adx=[x]0a=a−0=a
-
∫0ay2dy=[3y3]0a=3a3−303=3a3
-
∫0adz=[z]0a=a−0=a
Substitute these results back into the expression for UE: UE=29ϵ0(a)(3a3)(a) UE=29ϵ03a5 UE=23ϵ0a5
