Question
Question: A point charge q is placed at a distance R from the center O of a uniformly charged hemispherical sh...
A point charge q is placed at a distance R from the center O of a uniformly charged hemispherical shell of surface charge density σ and radius R on its axis of symmetry as shown in the figure. Then the net electric force experienced by the point charge q due to the uniformly charged hemispherical shell is
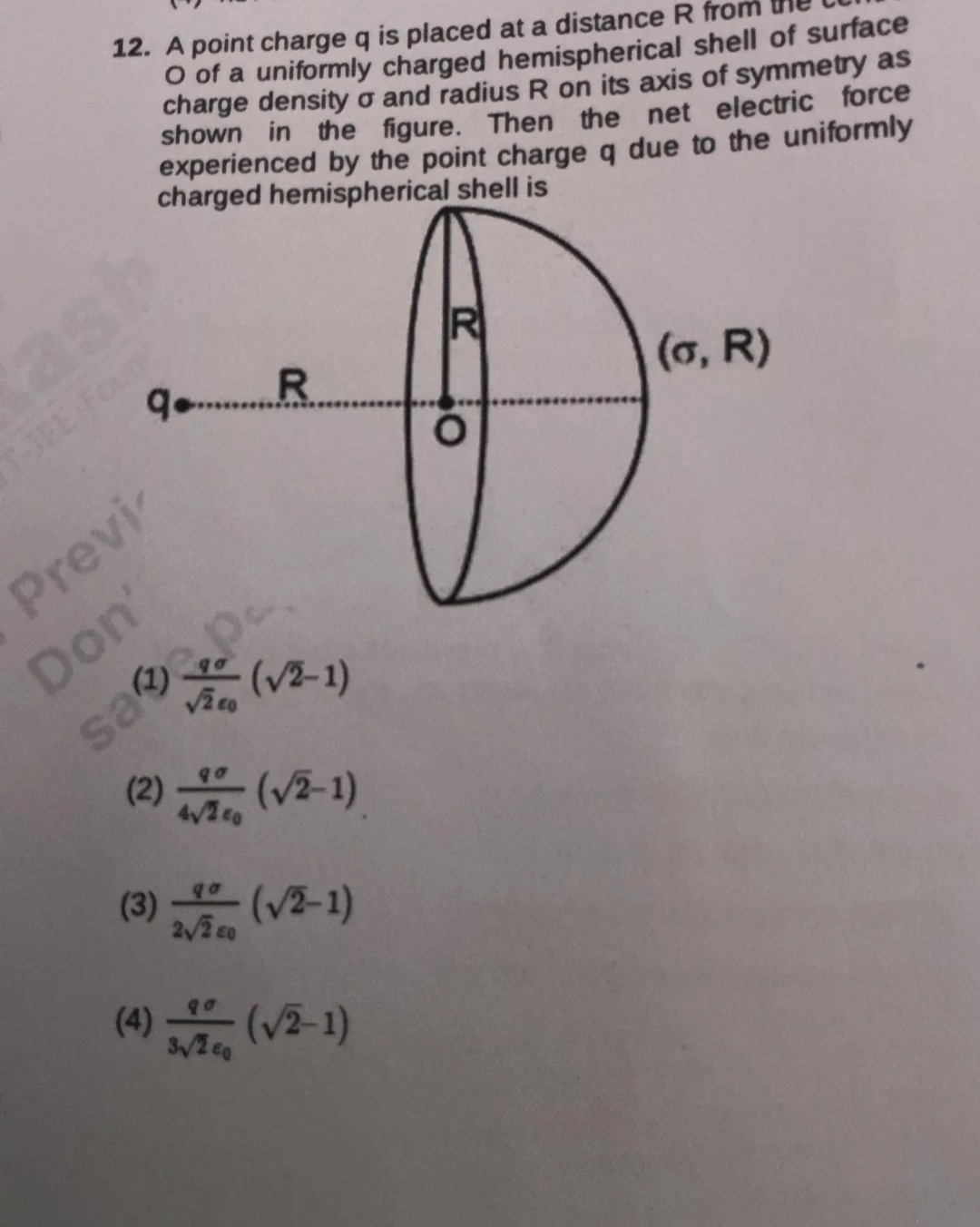
2ϵ0qσ(2−1)
42ϵ0qσ(2−1)
22ϵ0qσ(2−1)
32ϵ0qσ(2−1)
(3)
Solution
To find the net electric force experienced by the point charge q due to the uniformly charged hemispherical shell, we first need to calculate the electric field produced by the hemispherical shell at the location of the point charge.
Let the center of the hemispherical shell be at the origin O (0,0,0). Let the axis of symmetry be the x-axis. The hemispherical shell is on the positive x-axis side, meaning it extends from x=0 to x=R. The point charge q is located at (−R,0,0).
Consider a differential ring element on the hemispherical shell. Let this ring be at an angle θ with respect to the positive x-axis. The radius of this ring is r=Rsinθ. The width of the ring is Rdθ. The area of this differential ring element is dA=(2πRsinθ)(Rdθ)=2πR2sinθdθ. The charge on this ring element is dQ=σdA=2πR2σsinθdθ.
A point on this ring can be represented by coordinates (Rcosθ,Rsinθcosϕ,Rsinθsinϕ). The position of the point charge is (−R,0,0). The distance r′ from any point on the ring to the point charge q is: r′2=(Rcosθ−(−R))2+(Rsinθcosϕ−0)2+(Rsinθsinϕ−0)2 r′2=(R(1+cosθ))2+R2sin2θ(cos2ϕ+sin2ϕ) r′2=R2(1+2cosθ+cos2θ)+R2sin2θ r′2=R2(1+2cosθ+cos2θ+sin2θ) r′2=R2(2+2cosθ)=2R2(1+cosθ). Using the identity 1+cosθ=2cos2(θ/2), we get: r′2=2R2(2cos2(θ/2))=4R2cos2(θ/2). So, r′=2Rcos(θ/2). (Since for the hemisphere, θ ranges from 0 to π/2, θ/2 ranges from 0 to π/4, and cos(θ/2) is positive).
The electric field dE due to this ring element at the point charge q will have components perpendicular to the x-axis that cancel out due to symmetry when integrated over the entire ring. Only the x-component of the electric field will contribute to the net field.
The x-component of the electric field dEx due to a point charge dQ on the ring is given by dEx=4πϵ01r′2dQcosα, where α is the angle between the vector from dQ to q and the positive x-axis. The vector from a point on the ring (Rcosθ,Rsinθ,0) to q(−R,0,0) is (−R−Rcosθ,−Rsinθ,0). The x-component of this vector is −R(1+cosθ). So, cosα=r′−R(1+cosθ)=2Rcos(θ/2)−R(2cos2(θ/2))=−cos(θ/2). The negative sign indicates that the electric field is directed towards the negative x-axis (towards the hemisphere).
Now, substitute dQ, r′2, and cosα into the expression for dEx: dEx=4πϵ014R2cos2(θ/2)2πR2σsinθdθ(−cos(θ/2)) dEx=−4πϵ014R2cos(θ/2)2πR2σsinθdθ dEx=−8ϵ0σcos(θ/2)sinθdθ. Using the identity sinθ=2sin(θ/2)cos(θ/2): dEx=−8ϵ0σcos(θ/2)2sin(θ/2)cos(θ/2)dθ dEx=−4ϵ0σsin(θ/2)dθ.
To find the total electric field Ex, we integrate dEx over the entire hemisphere. The angle θ ranges from 0 (the tip of the hemisphere, x=R) to π/2 (the base of the hemisphere, x=0). Ex=∫0π/2−4ϵ0σsin(θ/2)dθ. Let u=θ/2, so du=21dθ⇒dθ=2du. When θ=0, u=0. When θ=π/2, u=π/4. Ex=∫0π/4−4ϵ0σsin(u)(2du) Ex=−2ϵ0σ∫0π/4sin(u)du Ex=−2ϵ0σ[−cos(u)]0π/4 Ex=2ϵ0σ[cos(u)]0π/4 Ex=2ϵ0σ(cos(π/4)−cos(0)) Ex=2ϵ0σ(21−1) Ex=−2ϵ0σ(1−21)=−2ϵ0σ(22−1) Ex=−22ϵ0σ(2−1).
The net electric force experienced by the point charge q is F=qEx. F=q(−22ϵ0σ(2−1)). The magnitude of the force is F=22ϵ0qσ(2−1).
Comparing this result with the given options: (1) 2ϵ0qσ(2−1) (2) 42ϵ0qσ(2−1) (3) 22ϵ0qσ(2−1) (4) 32ϵ0qσ(2−1)
The calculated magnitude matches option (3).
The final answer is (3)
Solution:
-
Define Coordinate System and Elements: Place the center of the hemispherical shell at the origin (0,0,0). The axis of symmetry is the x-axis, with the hemisphere extending for x≥0. The point charge q is at (−R,0,0). Consider a differential ring element on the hemisphere at angle θ from the positive x-axis.
- Area of ring dA=2πR2sinθdθ.
- Charge on ring dQ=σdA=2πR2σsinθdθ.
-
Distance and Angle: The distance r′ from any point on the ring to the point charge q is r′=2Rcos(θ/2). The angle α between the vector from dQ to q and the positive x-axis is such that cosα=−cos(θ/2).
-
Electric Field Contribution: By symmetry, only the x-component of the electric field contributes.
dEx=4πϵ01r′2dQcosα
Substitute dQ, r′, and cosα:
dEx=4πϵ01(2Rcos(θ/2))22πR2σsinθdθ(−cos(θ/2))
dEx=−4ϵ0σsin(θ/2)dθ.
-
Integration: Integrate dEx from θ=0 to θ=π/2 (for the hemisphere):
Ex=∫0π/2−4ϵ0σsin(θ/2)dθ
Let u=θ/2, du=(1/2)dθ. Limits: 0→π/4.
Ex=−2ϵ0σ∫0π/4sin(u)du=−2ϵ0σ[−cos(u)]0π/4
Ex=2ϵ0σ(cos(π/4)−cos(0))=2ϵ0σ(21−1)
Ex=−22ϵ0σ(2−1).
-
Net Force: The net electric force on charge q is F=qEx.
F=q(−22ϵ0σ(2−1)).
The magnitude of the force is F=22ϵ0qσ(2−1).
