Question

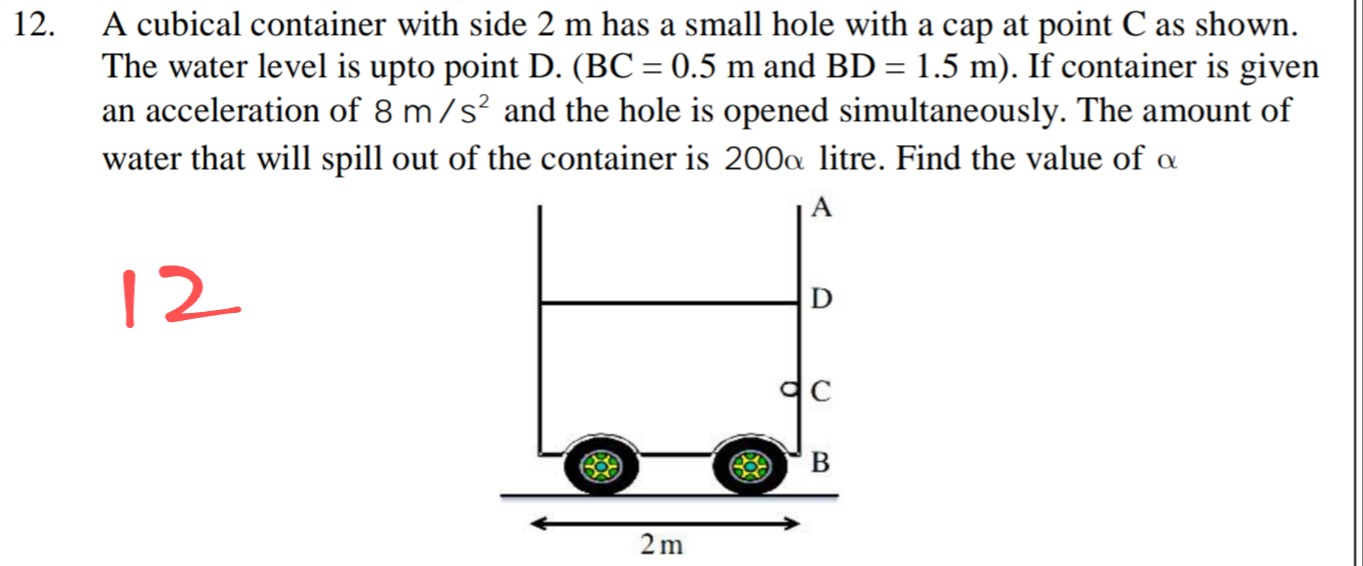
A cubical container with side 2 m has a small hole with a cap at point C as shown. The water level is upto point D. (BC = 0.5 m and BD = 1.5 m). If container is given an acceleration of 8 m/s² and the hole is opened simultaneously. The amount of water that will spill out of the container is 200$\alpha$ litre. Find the value of $\alpha$

Answer 1

6

Answer 2

Solution:

1. Initial and Final Volumes:

   • The cube (side = 2 m) is initially filled with water up to a horizontal free–surface. The given fact “BD = 1.5 m” tells us that the water–depth on the right–wall (from B, the bottom–right corner) is 1.5 m. Hence the initial water–volume is V_initial = (area of base) × (water–depth) = (2×2)×1.5 = 6 m³.

2. Effect of Acceleration:

   • When the container is accelerated horizontally with acceleration a = 8 m/s² (taking g = 10 m/s² as is customary in many JEE/NEET problems) the free–surface re–aligns perpendicular to the resultant acceleration. (Recall: In an accelerated frame the free–surface satisfies tan φ = a/g = 8/10 = 0.8 so that φ ≈ 38.66°.)
   • Thus the free–surface tilts with a constant slope 0.8 relative to the horizontal.

3. Determination of the Final Water Level:

   • Take x–axis along the horizontal from the right–wall (x = 0) to left–wall (x = 2). Because water spills out through the hole on the right side (point C on the right–wall is located 0.5 m above the bottom, i.e. BC = 0.5 m), the final water level on the right–wall adjusts to be just below the hole. Let the free–surface (which must be a plane of slope 0.8) be f(x) = H + 0.8 x.
   • Since the water cannot hang over the rim, at the left–wall (x = 2) the water just reaches the top: f(2) = H + 0.8×2 = H + 1.6 = 2.0 ⟹ H = 2.0 − 1.6 = 0.4 m.
   • Thus the final free–surface in the container is f(x) = 0.4 + 0.8 x.

4. Final Volume Calculation:

   • In the container the water fills completely below the tilted free–surface. Its volume is given by integrating over x (and multiplying by the depth 2 m in the third direction): V_final = 2 × ∫₀² f(x) dx = 2 × ∫₀² (0.4 + 0.8x) dx = 2 × [0.4x + 0.8·x²/2]₀² = 2 × [0.4×2 + 0.4×(2)²] = 2 × [0.8 + 1.6] = 2 × 2.4 = 4.8 m³.

5. Spilled Volume and α:

   • The amount of water spilled is the decrease in volume: ΔV = V_initial − V_final = 6 − 4.8 = 1.2 m³.
   • Since 1 m³ = 1000 litres, spilled water = 1.2×1000 = 1200 litres.
   • It is given that the water spilled equals 200α litres, so 200α = 1200 ⟹ α = 1200/200 = 6.

Summary of Key Points:

• Initially, water is filled to a horizontal depth of 1.5 m so that V_initial = 6 m³.
• Under acceleration, free–surface tilts with slope tanφ = 0.8.
• Final free–surface is f(x) = 0.4 + 0.8x (since f(2) = 2 m at the left rim).
• Final water–volume = 4.8 m³, so spill = 1.2 m³ = 1200 litres = 200×6 litres.
• Therefore, α = 6.