Question

A compound of vanadium has a magnetic moment ($\mu$) of 1.73 BM. If the vanadium ion in the compound is present as $V^{x+}$, then, the value of x is?

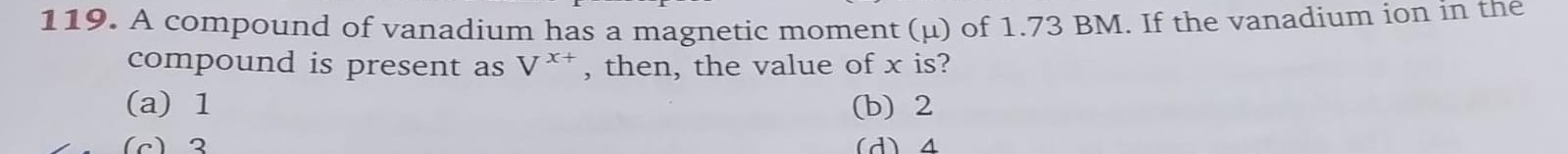
• A. 1
• B. 2
• C. 3
• D. 4

Answer 1

Answer: (D)

4

Answer 2

The magnetic moment ($\mu$) of a transition metal ion is given by the formula $\mu = \sqrt{n(n+2)}$ BM, where $n$ is the number of unpaired electrons. Given $\mu = 1.73$ BM: $1.73 = \sqrt{n(n+2)}$ $(1.73)^2 \approx n(n+2)$ $2.9929 \approx n(n+2)$ By inspection, if $n=1$, $n(n+2) = 1(1+2) = 3$. Thus, the number of unpaired electrons is $n=1$.

Vanadium (V) has atomic number 23, with electronic configuration $[Ar] 4s^2 3d^3$. We need to find the charge $x$ of the vanadium ion ($V^{x+}$) that results in 1 unpaired electron. Electrons are removed from the outermost shell ($4s$) first, followed by the $3d$ subshell.

• Neutral V: $[Ar] 4s^2 3d^3$ (3 unpaired electrons in $3d$)
• $V^{1+}$: $[Ar] 4s^1 3d^3$ (4 unpaired electrons)
• $V^{2+}$: $[Ar] 3d^3$ (3 unpaired electrons)
• $V^{3+}$: $[Ar] 3d^2$ (2 unpaired electrons)
• $V^{4+}$: $[Ar] 3d^1$ (1 unpaired electron)
• $V^{5+}$: $[Ar] 3d^0$ (0 unpaired electrons)

The configuration $[Ar] 3d^1$ yields $n=1$ unpaired electron, which matches the calculated value. This configuration corresponds to the $V^{4+}$ ion, meaning $x=4$.