Question
Question: If $\bar{a}$ = î - 2ĵ + 3k and $\bar{b}$ = 2î + 3ĵ − k are two vectors, then the angle between the v...
If aˉ = î - 2ĵ + 3k and bˉ = 2î + 3ĵ − k are two vectors, then the angle between the vectors 3aˉ + 5bˉ and 5aˉ + 3bˉ is
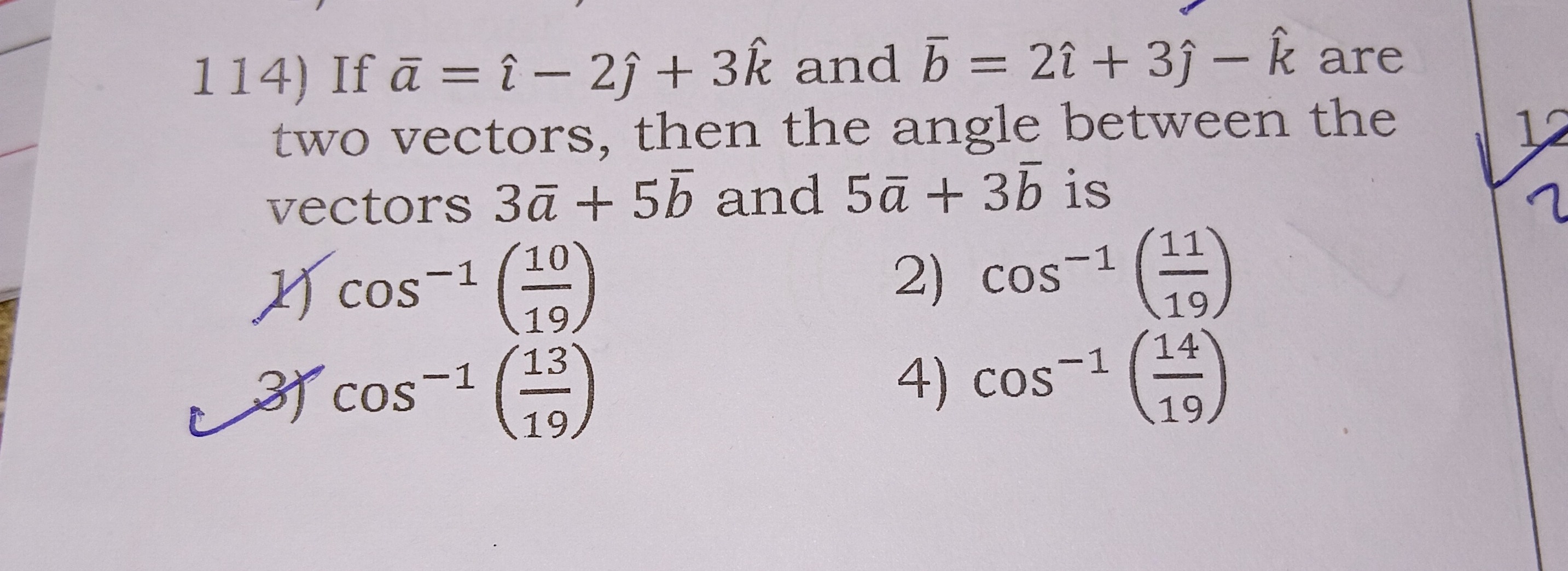
A
cos−1(1910)
B
cos−1(1911)
C
cos−1(1913)
D
cos−1(1914)
Answer
cos−1(1913)
Explanation
Solution
Let
a=⟨1,−2,3⟩,b=⟨2,3,−1⟩.
Compute
u=3a+5b=3⟨1,−2,3⟩+5⟨2,3,−1⟩=⟨3+10,−6+15,9−5⟩=⟨13,9,4⟩,
v=5a+3b=5⟨1,−2,3⟩+3⟨2,3,−1⟩=⟨5+6,−10+9,15−3⟩=⟨11,−1,12⟩.
Now, find the dot product:
u⋅v=(13)(11)+(9)(−1)+(4)(12)=143−9+48=182.
Determine the magnitudes:
∣u∣=132+92+42=169+81+16=266,
∣v∣=112+(−1)2+122=121+1+144=266.
Thus, the cosine of the angle θ between u and v is
cosθ=∣u∣∣v∣u⋅v=266182=13391=1913.
Hence,
θ=cos−1(1913).
