Question

Number of integral values of p for which the origin lies inside the triangle formed by the lines $L_1 : y + 3x = 9, L_2 : 2y - 3x = 18$ and $L_3 : y - px - 8p = -3$ are

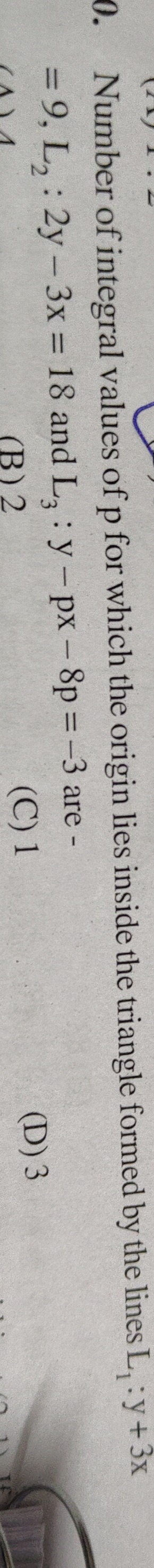
• A. 4
• B. 2
• C. 1
• D. 3

Answer 1

Answer: (D)

3

Answer 2

To find the number of integral values of 'p' for which the origin (0,0) lies inside the triangle formed by the given lines, we first define the lines and find the vertices of the triangle.

The given lines are: $L_1: 3x + y - 9 = 0$ $L_2: -3x + 2y - 18 = 0$ $L_3: -px + y - 8p + 3 = 0$

Let's find the vertices of the triangle:

1. Vertex A ($L_1 \cap L_2$): Adding $L_1$ and $L_2$: $(3x + y - 9) + (-3x + 2y - 18) = 0 \implies 3y - 27 = 0 \implies y = 9$. Substitute $y=9$ into $L_1$: $3x + 9 - 9 = 0 \implies 3x = 0 \implies x = 0$. So, Vertex A = (0, 9).

2. Vertex B ($L_2 \cap L_3$): From $L_3$: $y = px + 8p - 3$. Substitute into $L_2$: $-3x + 2(px + 8p - 3) - 18 = 0$ $-3x + 2px + 16p - 6 - 18 = 0$ $x(2p - 3) = 24 - 16p = 8(3 - 2p)$ If $2p - 3 \neq 0$, then $x = \frac{8(3 - 2p)}{2p - 3} = -8$. Substitute $x=-8$ into $y = px + 8p - 3$: $y = p(-8) + 8p - 3 = -8p + 8p - 3 = -3$. So, Vertex B = (-8, -3). This is valid for $p \neq 3/2$.

3. Vertex C ($L_3 \cap L_1$): From $L_1$: $y = 9 - 3x$. Substitute into $L_3$: $-px + (9 - 3x) - 8p + 3 = 0$ $x(-p - 3) + 12 - 8p = 0$ $x(p + 3) = 12 - 8p$ If $p + 3 \neq 0$, then $x = \frac{12 - 8p}{p+3}$. Substitute $x$ back into $y = 9 - 3x$: $y = 9 - 3\left(\frac{12 - 8p}{p+3}\right) = \frac{9(p+3) - 3(12 - 8p)}{p+3} = \frac{9p + 27 - 36 + 24p}{p+3} = \frac{33p - 9}{p+3}$. So, Vertex C = $\left(\frac{12 - 8p}{p+3}, \frac{33p - 9}{p+3}\right)$. This is valid for $p \neq -3$.

For the origin (0,0) to lie inside the triangle, it must lie on the same side of each line as the vertex opposite to that line. Let $L_i(x,y)$ be the expression for the line. We need $L_i(0,0)$ and $L_i(\text{opposite vertex})$ to have the same sign.

Condition 1: For $L_1$ (opposite vertex is B) $L_1(0,0) = 3(0) + 0 - 9 = -9$. $L_1(B) = 3(-8) + (-3) - 9 = -24 - 3 - 9 = -36$. Since both $L_1(0,0)$ and $L_1(B)$ are negative, they have the same sign. This condition is satisfied for all valid $p$.

Condition 2: For $L_2$ (opposite vertex is C) $L_2(0,0) = -3(0) + 2(0) - 18 = -18$. $L_2(C) = -3\left(\frac{12 - 8p}{p+3}\right) + 2\left(\frac{33p - 9}{p+3}\right) - 18$ $L_2(C) = \frac{-36 + 24p + 66p - 18 - 18(p+3)}{p+3}$ $L_2(C) = \frac{-36 + 24p + 66p - 18 - 18p - 54}{p+3} = \frac{72p - 108}{p+3}$. For the origin and C to be on the same side of $L_2$, $L_2(0,0)$ and $L_2(C)$ must have the same sign. Since $L_2(0,0) = -18$ (negative), we need $L_2(C) < 0$. $\frac{72p - 108}{p+3} < 0 \implies \frac{36(2p - 3)}{p+3} < 0$. This inequality holds when $(2p - 3)$ and $(p+3)$ have opposite signs: Case A: $2p - 3 > 0$ and $p+3 < 0 \implies p > 3/2$ and $p < -3$. No solution. Case B: $2p - 3 < 0$ and $p+3 > 0 \implies p < 3/2$ and $p > -3$. So, $-3 < p < 3/2$.

Condition 3: For $L_3$ (opposite vertex is A) $L_3(0,0) = -p(0) + 0 - 8p + 3 = 3 - 8p$. $L_3(A) = -p(0) + 9 - 8p + 3 = 12 - 8p$. For the origin and A to be on the same side of $L_3$, $L_3(0,0)$ and $L_3(A)$ must have the same sign. $(3 - 8p)(12 - 8p) > 0$. This inequality holds when $(3 - 8p)$ and $(12 - 8p)$ have the same sign: Case A: $3 - 8p > 0$ and $12 - 8p > 0 \implies p < 3/8$ and $p < 12/8 = 3/2$. Intersection: $p < 3/8$. Case B: $3 - 8p < 0$ and $12 - 8p < 0 \implies p > 3/8$ and $p > 3/2$. Intersection: $p > 3/2$. So, $p < 3/8$ or $p > 3/2$.

Combining all conditions: We need to find the values of $p$ that satisfy:

1. $-3 < p < 3/2$ (from Condition 2)
2. ($p < 3/8$ or $p > 3/2$) (from Condition 3)

The intersection of these two conditions is: $(-3, 3/2) \cap ((-\infty, 3/8) \cup (3/2, \infty))$ This simplifies to $(-3, 3/8)$.

We also need to ensure that a triangle is formed, which means $p \neq 3/2$ (to avoid $L_2$ and $L_3$ being identical) and $p \neq -3$ (to avoid $L_1$ and $L_3$ being parallel). The interval $(-3, 3/8)$ already excludes these values.

The integral values of $p$ in the interval $(-3, 3/8)$ are $-2, -1, 0$. There are 3 such integral values.