Question
Question: A smooth wedge of mass $m$ and angle of inclination 60° rests unattached between two springs of spri...
A smooth wedge of mass m and angle of inclination 60° rests unattached between two springs of spring constant k and 4k, on a smooth horizontal plane, both springs in the unextended position. The time period of small oscillations of the wedge (assuming that the springs are constrained to get compressed along their length) equals
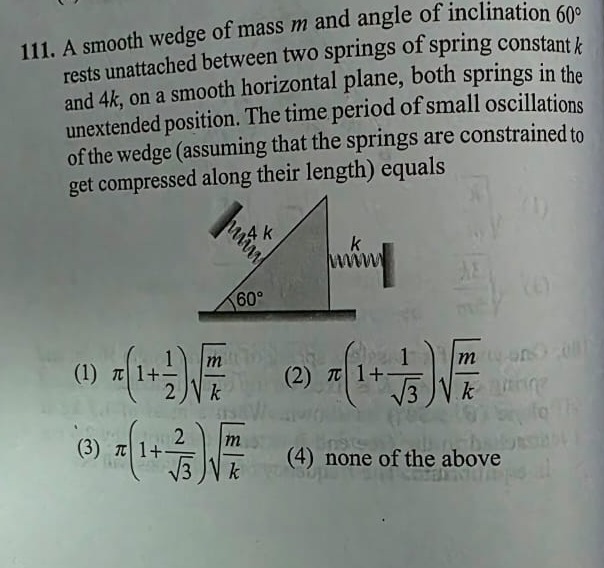
π(1+21)km
π(1+31)km
π(1+32)km
none of the above
π(1+32)km
Solution
The wedge has two contacts—a vertical face (with 4k) and an inclined face at 60° (with k). On a small horizontal displacement x, the left spring compresses by x. On the right, the sliding contact on the 60° face produces a compression that is less (by geometric projection) – effectively proportional to x/3. Adding the potential energies and comparing with 21keffx2, one finds an effective spring constant which yields a period T=π(1+32)km.
