Question
Question: There is a system of infinite pulleys and springs. Spring constants are in GP as k, 2k, 4k, 8k... sh...
There is a system of infinite pulleys and springs. Spring constants are in GP as k, 2k, 4k, 8k... shown in the figure. All the pulleys are massless and frictionless and strings are massless and inextensible. Then time period of oscillation will be? Mass of block is m.
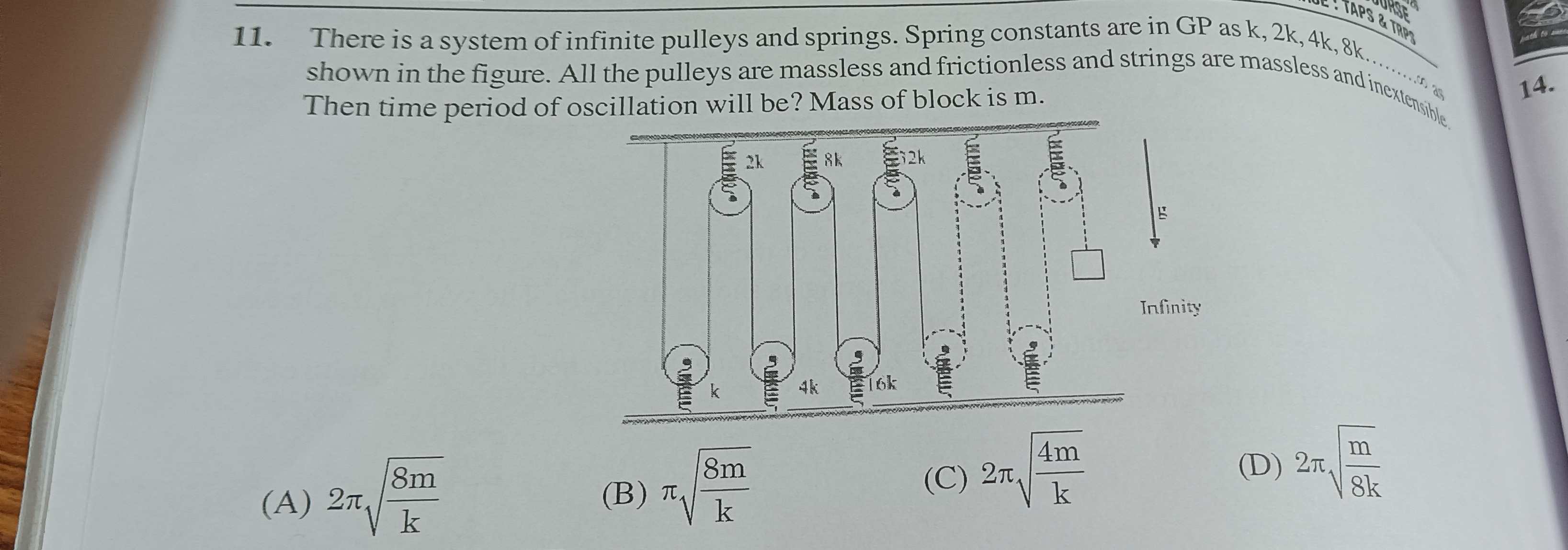
2πk8m
πk8m
2πk4m
2π8km
B
Solution
Let x be the downward displacement of the block from its equilibrium position. Let yn be the downward displacement of the center of the n-th movable pulley from its equilibrium position. From the geometry of the pulley system, if the block moves down by x, the first movable pulley moves down by y1=x/2. The center of the first pulley is attached to a string that goes over the second movable pulley. If the first pulley moves down by y1, the second movable pulley moves down by y2=y1/2=(x/2)/2=x/4. Similarly, y3=y2/2=(x/4)/2=x/8, and in general, yn=x/2n.
The springs are attached to the movable pulleys. The n-th spring has a spring constant kn=2n−1k. When the block is displaced by x, the n-th spring is stretched or compressed by yn=x/2n. The potential energy stored in the n-th spring is Un=21knyn2=21(2n−1k)(x/2n)2=212n−1k22nx2=21k22n2n−1x2=21k2n+11x2.
The total potential energy stored in all the springs is the sum of the potential energies in each spring: U=∑n=1∞Un=∑n=1∞21k2n+11x2=21kx2∑n=1∞2n+11. The sum is a geometric series with the first term (for n=1) a=1/21+1=1/4 and the common ratio r=1/2. The sum of an infinite geometric series is S=1−ra=1−1/21/4=1/21/4=21. So, the total potential energy is U=21kx2(21)=41kx2.
The restoring force on the block is F=−dxdU=−dxd(41kx2)=−41k(2x)=−21kx. The equation of motion for the block is mdt2d2x=F=−21kx. mdt2d2x+21kx=0. This is the equation of simple harmonic motion mdt2d2x+Keqx=0, where Keq is the equivalent spring constant. Comparing the equations, we have Keq=21k.
The angular frequency of oscillation is ω=mKeq=mk/2=2mk. The time period of oscillation is T=ω2π=2πk/2m=2πk2m.
Comparing with the options, option (B) is πk8m=π4⋅k2m=2πk2m. This matches our result.
Therefore, the correct answer is (B).
