Question

11. The number of ordered pairs (p, q), p, q ∈ N such that the equation x² – pqx + p + q = 0 has two integer roots.

Answer 1

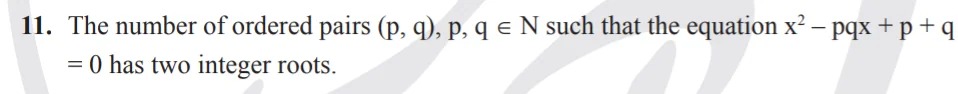
5

Answer 2

Solution:

We need (p, q) ∈ ℕ such that the quadratic

$$x^2 - (pq)x + (p+q)=0$$

has integer roots. Let the roots be α and β. Then by Vieta’s formulas,

$$\begin{cases} \alpha+\beta = pq \\ \alpha\beta = p+q \end{cases}$$

For fixed natural numbers p,q the discriminant of the quadratic is

$$D = p^2q^2 - 4(p+q).$$

For the equation to have integer roots, $D$ must be a perfect square.

A direct check for small values yields the following valid pairs:

• For $p=1$:
  $q=5$ gives $D=25-24=1$ (perfect square).

• For $p=2$:
  $q=2$ gives $D=16-16=0$ (double integer root),
  $q=3$ gives $D=36-20=16$ (perfect square).

• By symmetry, if $(p,q)=(1,5)$ then $(5,1)$ also works, and similarly $(p,q)=(2,3)$ gives $(3,2)$.

Thus the valid ordered pairs are:
$(1,5), (5,1), (2,2), (2,3), (3,2)$.

Explanation (minimal):

1. Set the quadratic $x^2 - pqx + (p+q)=0$ and denote its integer roots by α and β.
2. By Vieta: $\alpha+\beta=pq$ and $\alpha\beta=p+q$.
3. The discriminant is $p^2q^2-4(p+q)$ which must be a perfect square.
4. Testing small natural numbers, the only solutions found are: (1,5), (5,1), (2,2), (2,3), (3,2).

Answer: 5 ordered pairs.

Subject: Mathematics
Chapter: Quadratic Equations
Topic: Nature of Roots (using Vieta's relations)

Difficulty Level: Medium

Question Type: integer