Question
Question: $\int \sec^n x \tan x dx$ is equal to...
∫secnxtanxdx is equal to
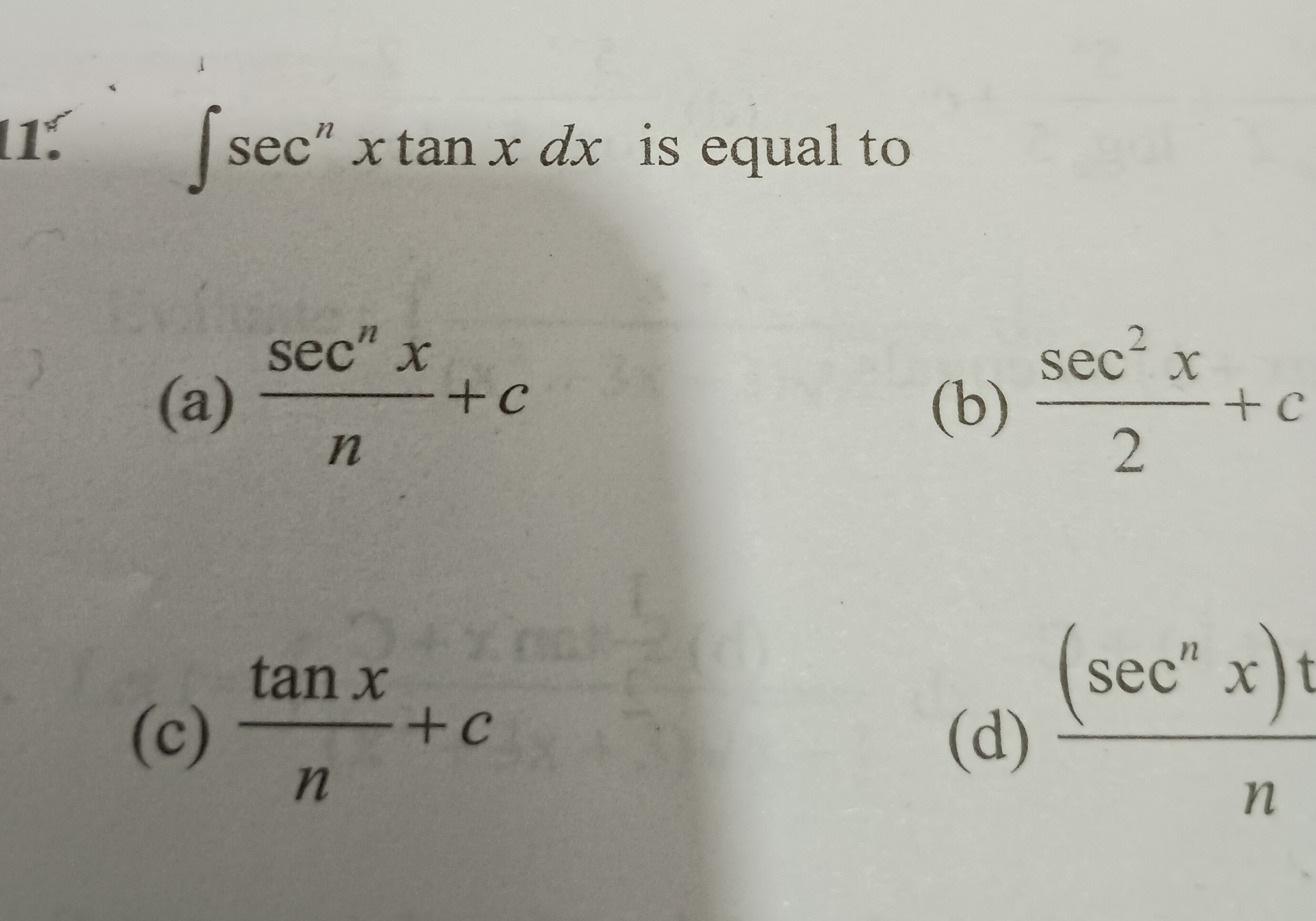
nsecnx+c
2sec2x+c
ntanx+c
n(secnx)
(a) nsecnx+c
Solution
To evaluate the integral ∫secnxtanxdx, we can use the method of substitution.
Let u=secx.
Now, differentiate u with respect to x:
dxdu=dxd(secx)=secxtanx.
From this, we can write du=secxtanxdx.
Now, rewrite the original integral by separating one secx term:
∫secnxtanxdx=∫secn−1x⋅(secxtanx)dx.
Substitute u=secx and du=secxtanxdx into the integral:
The integral becomes ∫un−1du.
Now, apply the power rule for integration, which states that ∫xkdx=k+1xk+1+C (for k=−1).
In our case, k=n−1. So,
∫un−1du=(n−1)+1u(n−1)+1+C=nun+C.
Finally, substitute back u=secx:
The integral evaluates to n(secx)n+C=nsecnx+C.
This result is valid for n=0.
Comparing this result with the given options:
(a) nsecnx+c
(b) 2sec2x+c
(c) ntanx+c
(d) n(secnx)
Option (a) matches our derived solution exactly, including the constant of integration 'c'. Option (d) is missing the constant of integration, which is conventionally included in indefinite integrals.
