Question

In the circuit shown in figure, battery and fuse is ideal. Fuse blows out when current in it exceeds 10 A

Switch S is closed at t = 0. Time in which fuse blows out is n seconds. Find the value of n

Answer 1

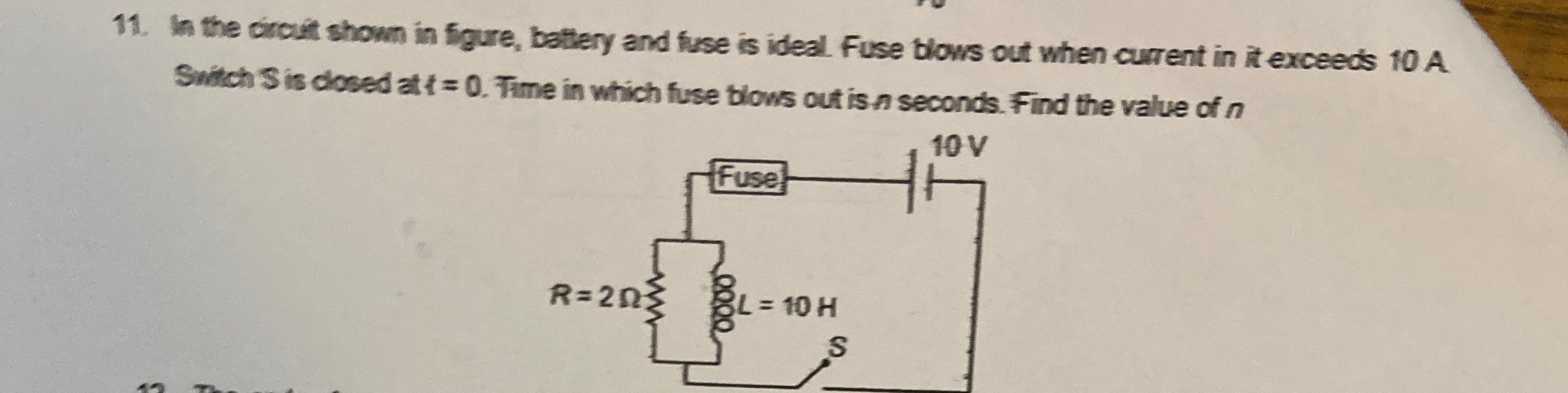
10

Answer 2

The circuit described is a series RL circuit connected to a DC voltage source.

Given parameters: Voltage of the battery, E = 10 V Resistance, R = 2 Ω Inductance, L = 10 H Fuse blows when current exceeds 10 A.

The current in a series RL circuit when a DC voltage E is applied at t = 0 is given by the formula: $I(t) = \frac{E}{R} (1 - e^{-Rt/L})$

First, let's calculate the maximum current that can flow in this circuit. This occurs as $t \to \infty$, where the exponential term $e^{-Rt/L}$ approaches 0. $I_{max} = \frac{E}{R} = \frac{10 \text{ V}}{2 \text{ Ω}} = 5 \text{ A}$

The fuse is rated to blow when the current exceeds 10 A. Since the maximum current that can ever flow in this circuit is 5 A, and 5 A is less than 10 A, the fuse will theoretically never blow if the resistance R = 2 Ω is considered.

However, the question asks for a specific value 'n' (time in seconds) for when the fuse blows, implying that it does blow. This suggests a potential inconsistency in the problem statement, or an implicit assumption that the resistance R is negligible (i.e., R=0), similar to how such problems are sometimes posed or as seen in the provided similar question where the coil had "zero resistance". To provide a numerical answer for 'n', we will proceed with the assumption that R=0, treating it as a purely inductive circuit.

Assuming R = 0 (purely inductive circuit): For a purely inductive circuit connected to a DC voltage source, the voltage across the inductor is equal to the applied voltage: $E = L \frac{dI}{dt}$

Substitute the given values for E and L: $10 \text{ V} = 10 \text{ H} \frac{dI}{dt}$

Solve for the rate of change of current: $\frac{dI}{dt} = \frac{10 \text{ V}}{10 \text{ H}} = 1 \text{ A/s}$

To find the current I(t) at time t, we integrate the rate of change of current. Assuming the current is 0 at t=0 (when the switch is closed): $\int_{0}^{I} dI = \int_{0}^{t} \frac{dI}{dt'} dt'$ $I(t) = \int_{0}^{t} 1 dt'$ $I(t) = t$

The fuse blows out when the current I(t) reaches 10 A. Set I(t) = 10 A: $10 \text{ A} = t \text{ seconds}$

Therefore, the time in which the fuse blows out is n = 10 seconds.

Explanation of the solution: The circuit is a series RL circuit. The current in such a circuit with a DC source approaches a maximum value of $E/R$. Given E=10V and R=2Ω, the maximum current is 5A. Since the fuse blows at 10A, theoretically, it would never blow. However, as the question asks for a specific time 'n', it implies the fuse does blow. This suggests an intended simplification where the resistance is negligible (R=0), similar to the provided similar question. Assuming R=0, the voltage across the inductor is $E = L \frac{dI}{dt}$. With E=10V and L=10H, $\frac{dI}{dt} = 1 \text{ A/s}$. Integrating this from t=0, the current is $I(t) = t$. For the fuse to blow at 10A, the time required is $t = 10 \text{ seconds}$.