Question
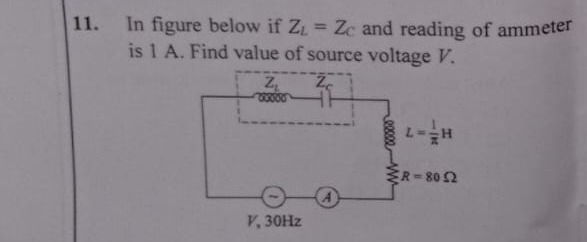
Question: In figure below if $Z_L = Z_c$ and reading of ammeter is 1 A. Find value of source voltage $V$. ...
In figure below if ZL=Zc and reading of ammeter is 1 A. Find value of source voltage V.
100 V
Solution
The circuit diagram shows a series AC circuit consisting of a resistor (R), an inductor (L), and a combination of another inductor (ZL) and a capacitor (ZC) connected in series. The source voltage is V at a frequency of 30 Hz, and the ammeter reading indicates the total current I=1 A.
Given values: Resistance R=80Ω Inductance L=π1 H Frequency f=30 Hz Current I=1 A
The problem states "if ZL=ZC". In the context of the diagram, ZL refers to the inductive reactance XL of the inductor inside the dashed box, and ZC refers to the capacitive reactance XC of the capacitor inside the dashed box. The condition ZL=ZC implies that the magnitudes of their reactances are equal, i.e., XL=XC.
These two components (ZL and ZC) are connected in series within the dashed box. The impedance of this series combination is given by: Zbox=jXL−jXC Since XL=XC, we have: Zbox=jXL−jXL=0 This means the portion of the circuit inside the dashed box acts as a short circuit at this frequency.
Therefore, the effective circuit consists only of the resistor R=80Ω and the inductor L=π1 H connected in series with the voltage source and ammeter.
First, calculate the angular frequency ω: ω=2πf=2π×30=60π rad/s
Next, calculate the inductive reactance of the inductor L=π1 H: XL=ωL=(60π)×(π1)=60Ω
Now, calculate the total impedance (Ztotal) of the series R-L circuit: Ztotal=R2+XL2 Ztotal=(80Ω)2+(60Ω)2 Ztotal=6400+3600 Ztotal=10000 Ztotal=100Ω
Finally, use Ohm's law for AC circuits to find the source voltage V: V=I×Ztotal V=1 A×100Ω V=100 V
The value of the source voltage V is 100 V.
