Solveeit Logo
Login

Question

Question: 11. If $\cos^{-1}x + \cos^{-1}y + \cos^{-1}z = \pi$, then...

  1. If cos⁡−1x+cos⁡−1y+cos⁡−1z=π\cos^{-1}x + \cos^{-1}y + \cos^{-1}z = \pi, then
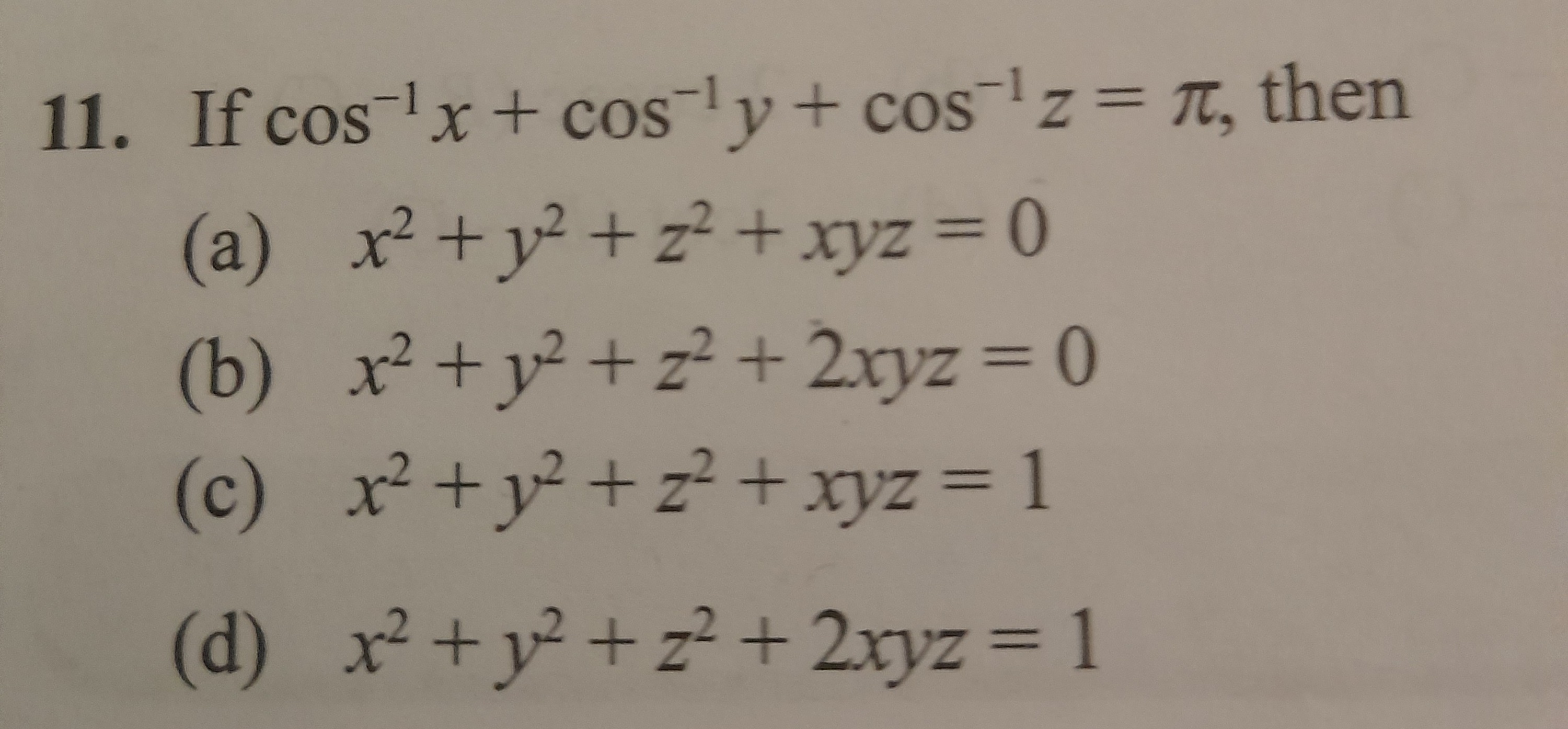
A

x2+y2+z2+xyz=0x^2 + y^2 + z^2 + xyz = 0

B

x2+y2+z2+2xyz=0x^2 + y^2 + z^2 + 2xyz = 0

C

x2+y2+z2+xyz=1x^2 + y^2 + z^2 + xyz = 1

D

x2+y2+z2+2xyz=1x^2 + y^2 + z^2 + 2xyz = 1

Answer

x2+y2+z2+2xyz=1x^2 + y^2 + z^2 + 2xyz = 1

Explanation

Solution

Solution Explanation:
Using the identity for inverse cosine functions, if

cos⁡−1x+cos⁡−1y+cos⁡−1z=π,\cos^{-1}x + \cos^{-1}y + \cos^{-1}z = \pi,

then it follows that

x2+y2+z2+2xyz=1.x^2+y^2+z^2+2xyz=1.

Answer: Option (d) x2+y2+z2+2xyz=1x^2+y^2+z^2+2xyz=1