Question

If A = tan 6° tan 42° and B = cot 66° cot 78°, then -

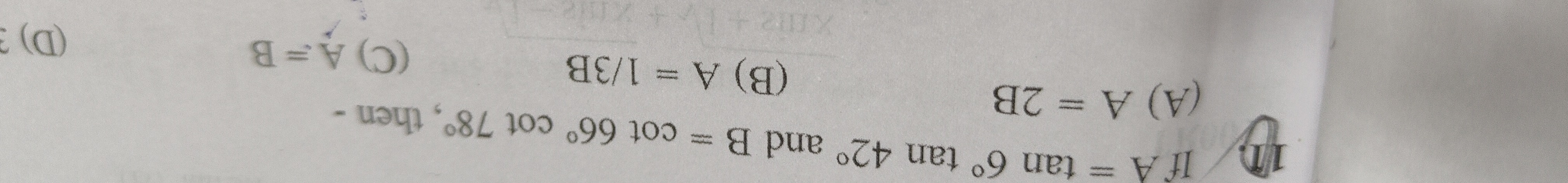
• A. A = 2B
• B. A = 1/3B
• C. A = B
• D. 3

Answer 1

Answer: (C)

A = B

Answer 2

Here's how to solve the problem:

1. Simplify B using the identity cot θ = tan (90° - θ):

   B = cot 66° cot 78°
   B = tan (90° - 66°) tan (90° - 78°)
   B = tan 24° tan 12°

2. Use the identity $\tan \theta \tan(60^\circ - \theta) \tan(60^\circ + \theta) = \tan(3\theta)$.

3. Apply for $\theta = 6^\circ$: $\tan 6^\circ \tan 54^\circ \tan 66^\circ = \tan 18^\circ$.

   Substitute $\tan 54^\circ = \cot 36^\circ = 1/\tan 36^\circ$ and $\tan 66^\circ = \cot 24^\circ = 1/\tan 24^\circ$.

   This yields $\tan 6^\circ \cdot \frac{1}{\tan 36^\circ} \cdot \frac{1}{\tan 24^\circ} = \tan 18^\circ$, so $\tan 6^\circ = \tan 18^\circ \tan 24^\circ \tan 36^\circ$.

4. Substitute this into A: $A = (\tan 18^\circ \tan 24^\circ \tan 36^\circ) \tan 42^\circ$.

5. Now compare A and B:

   $A = \tan 18^\circ \tan 24^\circ \tan 36^\circ \tan 42^\circ$
   $B = \tan 12^\circ \tan 24^\circ$

   Divide both by $\tan 24^\circ$:

   $A/\tan 24^\circ = \tan 18^\circ \tan 36^\circ \tan 42^\circ$
   $B/\tan 24^\circ = \tan 12^\circ$

6. Simplify $\tan 18^\circ \tan 36^\circ \tan 42^\circ$ using the same identity for $\theta = 18^\circ$:

   $\tan 18^\circ \tan(60^\circ - 18^\circ) \tan(60^\circ + 18^\circ) = \tan(3 \times 18^\circ)$
   $\tan 18^\circ \tan 42^\circ \tan 78^\circ = \tan 54^\circ$.

   So, $\tan 18^\circ \tan 42^\circ = \frac{\tan 54^\circ}{\tan 78^\circ} = \frac{\cot 36^\circ}{\cot 12^\circ} = \frac{\tan 12^\circ}{\tan 36^\circ}$.

7. Substitute this back: $\tan 18^\circ \tan 36^\circ \tan 42^\circ = (\tan 18^\circ \tan 42^\circ) \tan 36^\circ = \left(\frac{\tan 12^\circ}{\tan 36^\circ}\right) \tan 36^\circ = \tan 12^\circ$.

8. Thus, $A/\tan 24^\circ = \tan 12^\circ$, which is equal to $B/\tan 24^\circ$.

9. Therefore, A = B.