Question
Question: $\begin{vmatrix} a-b-c & 2a & 2a \\ 2b & b-c-a & 2b \\ 2c & 2c & c-a-b \end{vmatrix}$ = $(a+b+c)^3$...
a−b−c2b2c2ab−c−a2c2a2bc−a−b = (a+b+c)3
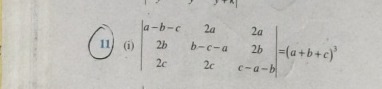
(a+b+c)3
Solution
To prove the identity:
a−b−c2b2c2ab−c−a2c2a2bc−a−b=(a+b+c)3
Let the given determinant be D.
D=a−b−c2b2c2ab−c−a2c2a2bc−a−b
Apply the row operation R1→R1+R2+R3:
D=(a−b−c)+2b+2c2b2c2a+(b−c−a)+2cb−c−a2c2a+2b+(c−a−b)2bc−a−b
Simplify the elements of the first row:
D=a+b+c2b2ca+b+cb−c−a2ca+b+c2bc−a−b
Take out the common factor (a+b+c) from R1:
D=(a+b+c)12b2c1b−c−a2c12bc−a−b
Apply the column operations C2→C2−C1 and C3→C3−C1:
D=(a+b+c)12b2c1−1(b−c−a)−2b2c−2c1−12b−2b(c−a−b)−2c
Simplify the elements:
D=(a+b+c)12b2c0−a−b−c000−a−b−c
D=(a+b+c)12b2c0−(a+b+c)000−(a+b+c)
This is a lower triangular matrix. The determinant of a triangular matrix is the product of its diagonal elements.
D=(a+b+c)×[1×(−(a+b+c))×(−(a+b+c))]
D=(a+b+c)×(a+b+c)2
D=(a+b+c)3
Thus, the identity is proven.
