Solveeit Logo
Login

Question

Question: Coordinates of the centre of a circle, whose radius is 2 unit and which touches the line pal \(x^2-y...

Coordinates of the centre of a circle, whose radius is 2 unit and which touches the line pal x2−y2−2x+1=0x^2-y^2 - 2x + 1 = 0 are:

A

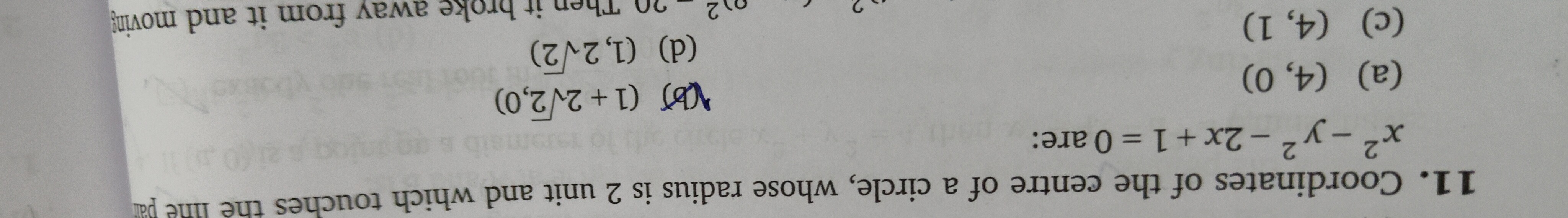
(4,0)

B

(1+2√2,0)

C

(4, 1)

D

(1,2√2)

Answer

The possible coordinates for the center of the circle are (1 + 2√2, 0) and (1, 2√2).

Explanation

Solution

The given equation x2−y2−2x+1=0x^2 - y^2 - 2x + 1 = 0 can be rewritten as (x−1)2−y2=0(x-1)^2 - y^2 = 0, which factors into two lines: L1:x−y−1=0L_1: x - y - 1 = 0 and L2:x+y−1=0L_2: x + y - 1 = 0. The center (h,k)(h, k) of a circle with radius r=2r=2 that touches both lines must be equidistant from them, with the distance being equal to the radius. The distance from (h,k)(h, k) to L1L_1 is ∣h−k−1∣12+(−1)2=∣h−k−1∣2\frac{|h - k - 1|}{\sqrt{1^2 + (-1)^2}} = \frac{|h - k - 1|}{\sqrt{2}}. The distance from (h,k)(h, k) to L2L_2 is ∣h+k−1∣12+12=∣h+k−1∣2\frac{|h + k - 1|}{\sqrt{1^2 + 1^2}} = \frac{|h + k - 1|}{\sqrt{2}}. Setting these distances equal to the radius 2:

  1. ∣h−k−1∣2=2  ⟹  ∣h−k−1∣=22\frac{|h - k - 1|}{\sqrt{2}} = 2 \implies |h - k - 1| = 2\sqrt{2}
  2. ∣h+k−1∣2=2  ⟹  ∣h+k−1∣=22\frac{|h + k - 1|}{\sqrt{2}} = 2 \implies |h + k - 1| = 2\sqrt{2}

Solving these equations by considering all four sign combinations for the absolute values yields the possible centers:

  • Case 1: h−k−1=22h - k - 1 = 2\sqrt{2} and h+k−1=22h + k - 1 = 2\sqrt{2}. Adding these gives 2h−2=422h - 2 = 4\sqrt{2}, so h=1+22h = 1 + 2\sqrt{2}. Substituting back gives k=0k=0. Center: (1+22,0)(1 + 2\sqrt{2}, 0).
  • Case 2: h−k−1=22h - k - 1 = 2\sqrt{2} and h+k−1=−22h + k - 1 = -2\sqrt{2}. Adding these gives 2h−2=02h - 2 = 0, so h=1h = 1. Substituting back gives k=−22k=-2\sqrt{2}. Center: (1,−22)(1, -2\sqrt{2}).
  • Case 3: h−k−1=−22h - k - 1 = -2\sqrt{2} and h+k−1=22h + k - 1 = 2\sqrt{2}. Adding these gives 2h−2=02h - 2 = 0, so h=1h = 1. Substituting back gives k=22k=2\sqrt{2}. Center: (1,22)(1, 2\sqrt{2}).
  • Case 4: h−k−1=−22h - k - 1 = -2\sqrt{2} and h+k−1=−22h + k - 1 = -2\sqrt{2}. Adding these gives 2h−2=−422h - 2 = -4\sqrt{2}, so h=1−22h = 1 - 2\sqrt{2}. Substituting back gives k=0k=0. Center: (1−22,0)(1 - 2\sqrt{2}, 0).

The possible centers are (1+22,0)(1 + 2\sqrt{2}, 0) and (1,22)(1, 2\sqrt{2}), which correspond to options (b) and (d). The extraneous text "g^2 - 20 Then it broke away from it and moving" is disregarded.