Question
Question: A ball is thrown straight upward with a speed v from a point h meter above the ground is: taken for ...
A ball is thrown straight upward with a speed v from a point h meter above the ground is: taken for the ball to strike the ground is:
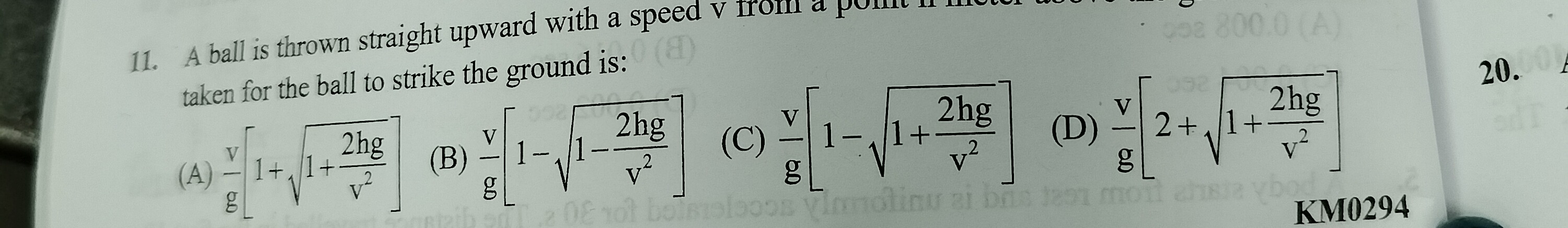
gv[1+1+v22hg]
gv[1−1−v22hg]
gv[1−1+v22hg]
gv[2+1+v22hg]
gv[1+1+v22hg]
Solution
Let's set up a coordinate system with the origin at the ground and the upward direction as positive.
The initial position of the ball is y0=h.
The initial velocity of the ball is v0=+v (since it is thrown straight upward).
The acceleration due to gravity is a=−g (acting downward).
We want to find the time t when the ball strikes the ground, which means its position is y(t)=0.
We use the kinematic equation relating position, initial position, initial velocity, acceleration, and time:
y(t)=y0+v0t+21at2
Substitute the known values:
0=h+vt+21(−g)t2
0=h+vt−21gt2
Rearrange the equation into a standard quadratic form At2+Bt+C=0:
21gt2−vt−h=0
This is a quadratic equation for t with coefficients A=2g, B=−v, and C=−h.
We can solve for t using the quadratic formula t=2A−B±B2−4AC:
t=2(2g)−(−v)±(−v)2−4(2g)(−h)
t=gv±v2+2gh
This gives two possible solutions for t:
t1=gv+v2+2gh
t2=gv−v2+2gh
Since v>0, g>0, and h>0, the term v2+2gh is real and positive.
Also, v2+2gh>v2, which implies v2+2gh>v2=v (assuming v>0).
Therefore, v−v2+2gh is a negative quantity.
So, t2=gv−v2+2gh is negative. Time t is the duration after the ball is thrown, so it must be positive. The negative solution represents a time before the ball was thrown, which is not relevant to the problem.
The physically relevant solution is the positive one:
t=gv+v2+2gh
Now, we need to check which option matches this result. Let's rewrite the expression to match the form of option (A):
t=gv+gv2+2gh
We can factor out gv from the expression:
t=gv(vv+vv2+2gh)
t=gv(1+v2v2+2gh) (assuming v>0)
t=gv(1+v2v2+2gh)
t=gv(1+v2v2+v22gh)
t=gv[1+1+v22gh]
This expression matches option (A).
