Question
Question: 9(4-1/x) + 5(6-1/x) < 4(9-1/x)...
9(4-1/x) + 5(6-1/x) < 4(9-1/x)
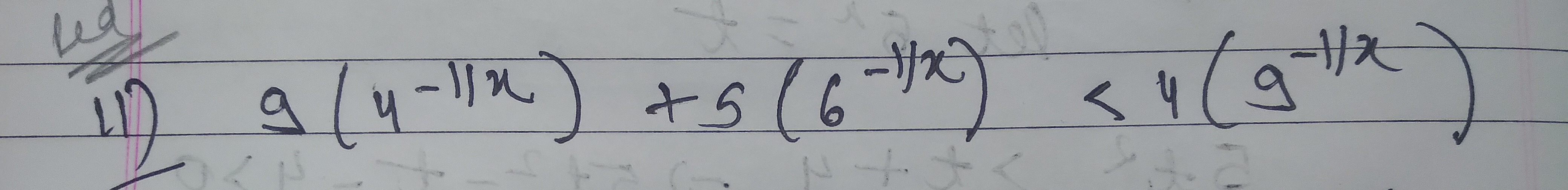
(-1/2, 0)
Solution
Let y=−1/x. The inequality becomes 9(4y)+5(6y)<4(9y). Divide by 9y (which is always positive): 9(94)y+5(96)y<4 9((32)2)y+5(32)y<4 9(32)2y+5(32)y<4
Let z=(32)y. Since z is an exponential term with a positive base, z>0. The inequality in terms of z is: 9z2+5z<4 9z2+5z−4<0
To find the roots of 9z2+5z−4=0: Using the quadratic formula z=2a−b±b2−4ac: z=2(9)−5±52−4(9)(−4)=18−5±25+144=18−5±169=18−5±13 The roots are z1=18−5+13=188=94 and z2=18−5−13=18−18=−1.
Since the quadratic 9z2+5z−4 has a positive leading coefficient (9), the inequality 9z2+5z−4<0 holds for z between the roots: −1<z<94
Considering z>0, we have 0<z<94. Substitute back z=(32)y: 0<(32)y<94
The inequality (32)y>0 is always true. We solve (32)y<94. Since 94=(32)2, we have: (32)y<(32)2
Because the base 32 is between 0 and 1, the inequality of the exponents is reversed: y>2
Substitute back y=−1/x: −x1>2
To solve this inequality: x−1−2>0 x−1−2x>0 Multiplying the numerator and denominator by -1 to make the numerator positive: x1+2x<0
This rational inequality is satisfied when the numerator and denominator have opposite signs. The critical points are x=0 and 1+2x=0⟹x=−1/2. We analyze the sign of x1+2x in the intervals (−∞,−1/2), (−1/2,0), and (0,∞).
- For x<−1/2: Let x=−1. −11+2(−1)=−1−1=1>0.
- For −1/2<x<0: Let x=−1/4. −1/41+2(−1/4)=−1/41−1/2=−1/41/2=−2<0. This interval satisfies the inequality.
- For x>0: Let x=1. 11+2(1)=13=3>0.
Therefore, the solution to the inequality is −1/2<x<0.
