Question
Question: $10\sin^4\theta + 15\cos^4\theta = 6$ $\frac{27\operatorname{cosec}^6\theta + 8\sec^6\theta}{16\se...
10sin4θ+15cos4θ=6
16sec8θ27cosec6θ+8sec6θ
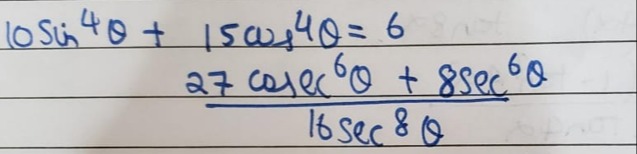
52
Solution
To solve the problem, we first need to find the values of sin2θ and cos2θ from the given equation, and then substitute them into the expression to be evaluated.
Step 1: Solve the given equation for sin2θ and cos2θ. The given equation is: 10sin4θ+15cos4θ=6
Divide the entire equation by cos4θ (assuming cosθ=0): 10cos4θsin4θ+15cos4θcos4θ=cos4θ6 10tan4θ+15=6sec4θ
We know the identity sec2θ=1+tan2θ. So, sec4θ=(1+tan2θ)2. Substitute this into the equation: 10tan4θ+15=6(1+tan2θ)2
Let x=tan2θ. The equation becomes a quadratic in x: 10x2+15=6(1+x)2 10x2+15=6(1+2x+x2) 10x2+15=6+12x+6x2 Rearrange the terms to form a standard quadratic equation: 4x2−12x+9=0
This quadratic equation is a perfect square: (2x−3)2=0. Solving for x: 2x−3=0 2x=3 x=23
So, we have tan2θ=23.
Now, we can find sin2θ and cos2θ using tan2θ=cos2θsin2θ and sin2θ+cos2θ=1. From tan2θ=23: cos2θsin2θ=23 2sin2θ=3cos2θ
Substitute cos2θ=1−sin2θ: 2sin2θ=3(1−sin2θ) 2sin2θ=3−3sin2θ 5sin2θ=3 sin2θ=53
Now find cos2θ: cos2θ=1−sin2θ=1−53=52
Step 2: Evaluate the given expression. The expression to evaluate is: 16sec8θ27cosec6θ+8sec6θ
We know that cosecθ=sinθ1 and secθ=cosθ1. So, cosec6θ=(sin2θ)−3 and sec6θ=(cos2θ)−3 and sec8θ=(cos2θ)−4.
Substitute the values of sin2θ=53 and cos2θ=52: =16(52)−427(53)−3+8(52)−3 =16(25)427(35)3+8(25)3 =16×245427×3353+8×2353 =16×1662527×27125+8×8125 =625125+125 =625250
Simplify the fraction: Divide both numerator and denominator by 25: =2510 Divide both numerator and denominator by 5: =52
The final answer is 52.
The final answer is 52.
Explanation of the solution:
- Transform the given equation 10sin4θ+15cos4θ=6 into a quadratic equation in terms of tan2θ by dividing by cos4θ and using sec2θ=1+tan2θ.
- Solve the quadratic equation (2tan2θ−3)2=0 to find tan2θ=23.
- Use tan2θ=cos2θsin2θ and sin2θ+cos2θ=1 to determine sin2θ=53 and cos2θ=52.
- Substitute these values into the expression 16sec8θ27cosec6θ+8sec6θ, rewriting terms as powers of sin2θ and cos2θ.
- Evaluate the numerical expression to get 625250, which simplifies to 52.
Answer: 52
