Question

An equi-convex lens of refractive index 1.5 and focal length 20cm is silvered on one side as shown in figure. At what distance 'x' an object should be kept so that the image is formed on the object?

Answer 1

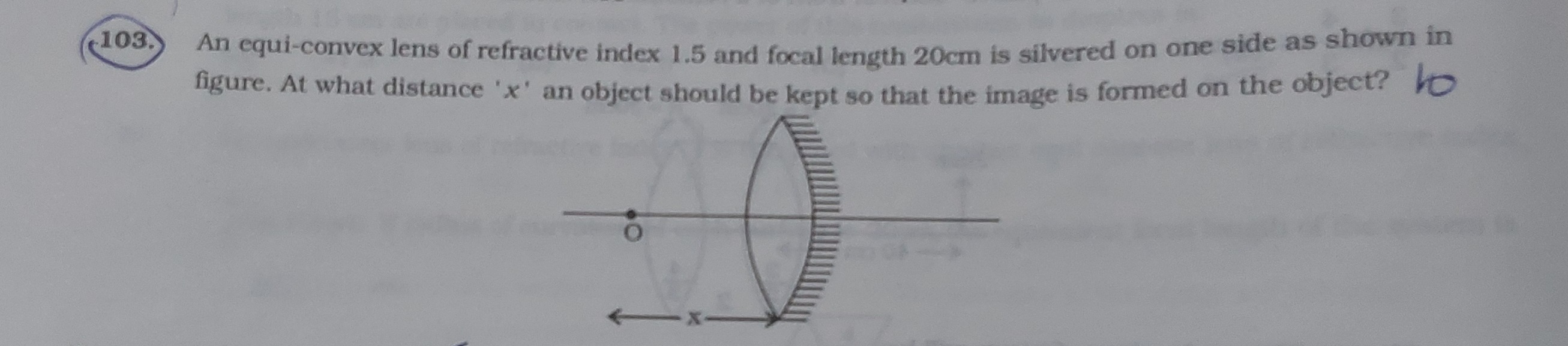
20 cm

Answer 2

The problem describes an equi-convex lens of refractive index $\mu = 1.5$ and focal length $f_L = 20$ cm, silvered on one side. We need to find the distance 'x' at which an object should be placed so that its image is formed on the object itself.

For the image to be formed on the object itself, the light rays must retrace their path. This condition is met if, after passing through the lens, the rays strike the silvered surface normally. For a spherical mirror, rays strike the surface normally if they are directed towards (or appear to come from) its center of curvature.

Let's break down the process:

1. First Refraction (from air to lens): Light travels from the object, through the first surface of the lens.

2. Reflection (from silvered surface): The light then reflects off the silvered surface.

3. Second Refraction (from lens to air): The reflected light passes back through the first surface of the lens.

Step 1: Calculate the radius of curvature (R) of the lens surfaces.

For an equi-convex lens, the radii of curvature are $R_1 = R$ and $R_2 = -R$. The lens maker's formula is: $\frac{1}{f_L} = (\mu - 1) \left(\frac{1}{R_1} - \frac{1}{R_2}\right)$

Given $f_L = 20$ cm and $\mu = 1.5$: $\frac{1}{20} = (1.5 - 1) \left(\frac{1}{R} - \frac{1}{-R}\right)$ $\frac{1}{20} = (0.5) \left(\frac{2}{R}\right)$ $\frac{1}{20} = \frac{1}{R}$ So, $R = 20$ cm.

Step 2: Apply the condition for image formation on the object.

For the final image to be formed on the object, the light rays must retrace their path. This happens if the rays, after the first refraction through the lens, strike the silvered surface normally.

The silvered surface is the right convex surface of the lens. It acts as a convex mirror.

For rays to strike a convex mirror normally, they must be converging towards its center of curvature.

The center of curvature of this convex mirror is located at a distance $R$ from the lens (to the right, assuming the lens is thin and its optical center is at the origin).

So, the image formed by the first refraction ($I_1$) must be located at $v_1 = +R = +20$ cm.

Step 3: Use the lens formula for the first refraction.

The object is placed at a distance 'x' from the lens, so $u = -x$.

The first surface of the lens has radius $R_1 = +R = +20$ cm.

The formula for refraction at a spherical surface is: $\frac{\mu_2}{v_1} - \frac{\mu_1}{u} = \frac{\mu_2 - \mu_1}{R_1}$

Here, $\mu_1 = 1$ (air), $\mu_2 = 1.5$ (glass). $\frac{1.5}{v_1} - \frac{1}{-x} = \frac{1.5 - 1}{+20}$ $\frac{1.5}{v_1} + \frac{1}{x} = \frac{0.5}{20} = \frac{1}{40}$

Now, substitute $v_1 = +20$ cm into this equation: $\frac{1.5}{20} + \frac{1}{x} = \frac{1}{40}$ $\frac{3}{40} + \frac{1}{x} = \frac{1}{40}$ $\frac{1}{x} = \frac{1}{40} - \frac{3}{40}$ $\frac{1}{x} = -\frac{2}{40}$ $\frac{1}{x} = -\frac{1}{20}$ $x = -20$ cm.

The negative sign indicates that the object should be placed on the side from which light is incident, which is consistent with the diagram. The distance is 20 cm.

Therefore, the object should be placed at $x=20$ cm from the lens.