Question
Question: Value of $\left(\frac{\sqrt{6}}{\sqrt{3}-\sqrt{2}+\frac{\sqrt{6}}{\sqrt{3}-\sqrt{2}+\frac{\sqrt{6}}{...
Value of 3−2+3−2+(3−2)+...6662 is
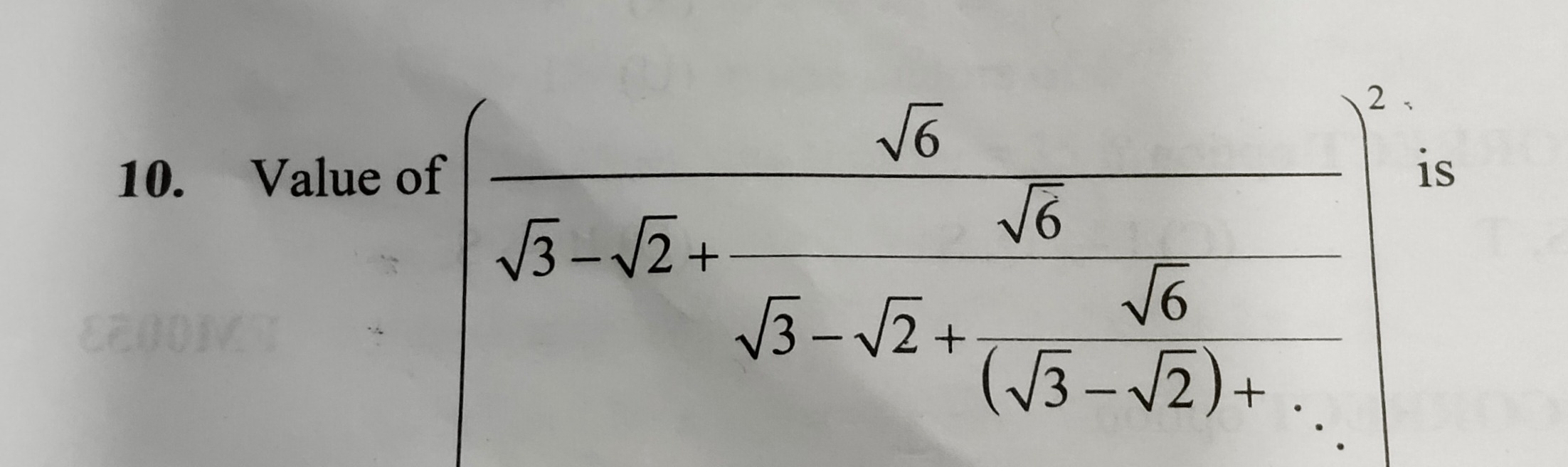
2
Solution
Let the given expression inside the square be y.
The expression is
y=3−2+3−2+(3−2)+...666
This is a continued fraction. Let a=3−2. The expression can be written as
y=a+a+a+...666
The structure of the continued fraction implies that the part starting from the second term in the denominator is the same as the original expression y.
So, we can write the equation:
y=a+y6
To solve for y, we multiply both sides by (a+y):
y(a+y)=6
ay+y2=6
Rearranging the terms, we get a quadratic equation in y:
y2+ay−6=0
Substitute the value of a=3−2:
y2+(3−2)y−6=0
We can solve this quadratic equation for y using the quadratic formula y=2a−b±b2−4ac, where in this case, the variable is y, and the coefficients are 1, (3−2), and −6.
Here, aquad=1, bquad=3−2, cquad=−6.
y=2(1)−(3−2)±(3−2)2−4(1)(−6)
First, calculate the term under the square root:
(3−2)2−4(−6)=(3)2−2(3)(2)+(2)2+46
=3−26+2+46
=5+26
Now, we need to find the square root of 5+26. We look for two numbers whose sum is 5 and product is 6. These numbers are 3 and 2.
5+26=3+2+232=(3+2)2=3+2 (since 3+2 is positive).
Substitute this back into the quadratic formula for y:
y=2−(3−2)±(3+2)
This gives two possible values for y:
y1=2−(3−2)+(3+2)=2−3+2+3+2=222=2
y2=2−(3−2)−(3+2)=2−3+2−3−2=2−23=−3
The given expression is a continued fraction of the form q+q+...pp where p=6>0 and q=3−2=3+21>0. A continued fraction of this form with positive terms converges to a positive value. Therefore, the value of y must be positive.
Comparing the two solutions, y1=2 is positive, while y2=−3 is negative.
Thus, the correct value for y is 2.
The question asks for the value of the square of the given expression, which is y2.
y2=(2)2=2
