Question

The x-coordinate of the center of the circle in the first quadrant (see figure) tangent to the lines $y = \frac{1}{2}x, y = 4$ and the x-axis is

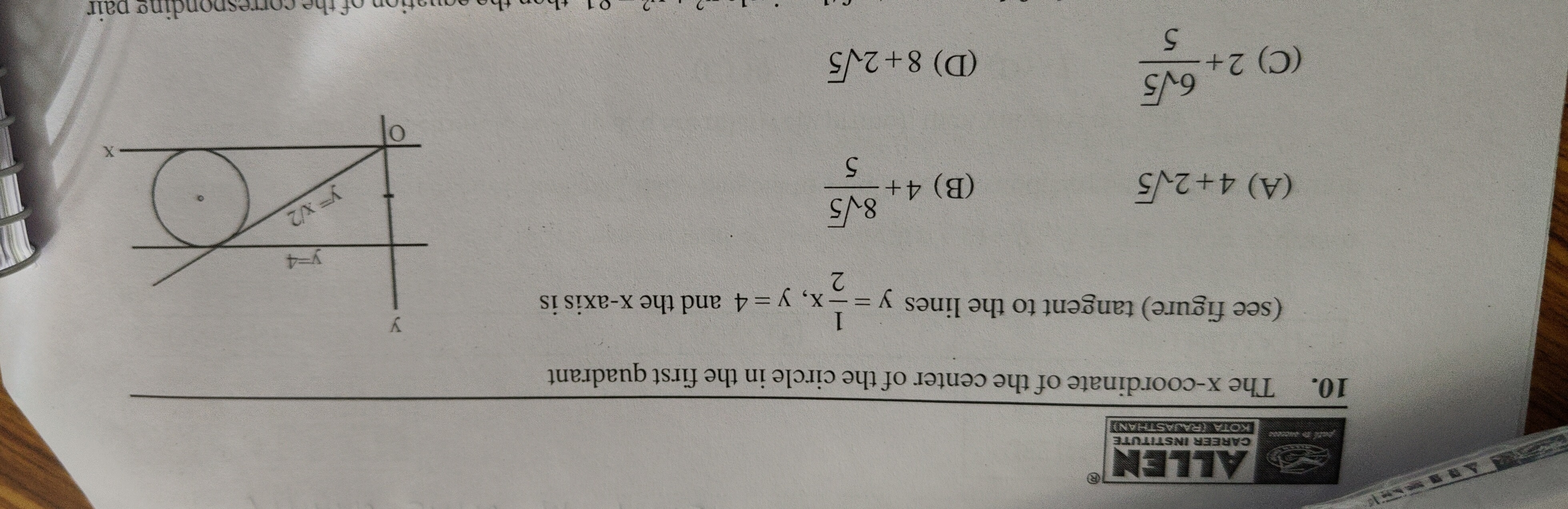
• A. 4+2\sqrt{5}
• B. 4 + \frac{8\sqrt{5}}{5}
• C. 2 + \frac{6\sqrt{5}}{5}
• D. 8+2\sqrt{5}

Answer 1

Answer: (A)

4+2\sqrt{5}

Answer 2

Let the center of the circle be $(h, k)$ and its radius be $r$. Since the circle is tangent to the x-axis ($y=0$) and the line $y=4$, and it is in the first quadrant, the y-coordinate of its center must be exactly in the middle of these two lines, so $k = \frac{0+4}{2} = 2$. The radius of the circle is the distance from the center to the x-axis, so $r = k = 2$.

The center of the circle is $(h, 2)$ and its radius is $r=2$. The circle is also tangent to the line $y = \frac{1}{2}x$. We can rewrite this line in the general form $Ax + By + C = 0$ as $x - 2y = 0$. The distance from the center $(h, 2)$ to the line $x - 2y = 0$ must be equal to the radius $r=2$. The distance formula from a point $(x_0, y_0)$ to a line $Ax + By + C = 0$ is $\frac{|Ax_0 + By_0 + C|}{\sqrt{A^2 + B^2}}$. Here, $(x_0, y_0) = (h, 2)$, $A=1$, $B=-2$, and $C=0$. The distance is $\frac{|1 \cdot h - 2 \cdot 2 + 0|}{\sqrt{1^2 + (-2)^2}} = \frac{|h - 4|}{\sqrt{1+4}} = \frac{|h - 4|}{\sqrt{5}}$. Setting this distance equal to the radius $r=2$: $\frac{|h - 4|}{\sqrt{5}} = 2$ $|h - 4| = 2\sqrt{5}$

This equation gives two possible values for $h$:

1. $h - 4 = 2\sqrt{5} \implies h = 4 + 2\sqrt{5}$
2. $h - 4 = -2\sqrt{5} \implies h = 4 - 2\sqrt{5}$

Since the circle is in the first quadrant, its x-coordinate of the center, $h$, must be positive. $4 + 2\sqrt{5}$ is clearly positive. For $h = 4 - 2\sqrt{5}$, we know that $\sqrt{5} \approx 2.236$, so $2\sqrt{5} \approx 4.472$. Thus, $h \approx 4 - 4.472 = -0.472$, which is negative. Therefore, $h = 4 - 2\sqrt{5}$ is not a valid solution for a circle in the first quadrant. The only valid x-coordinate for the center is $h = 4 + 2\sqrt{5}$.