Question

The velocity-time graph of body is shown in figure. Which of the following statements is wrong?

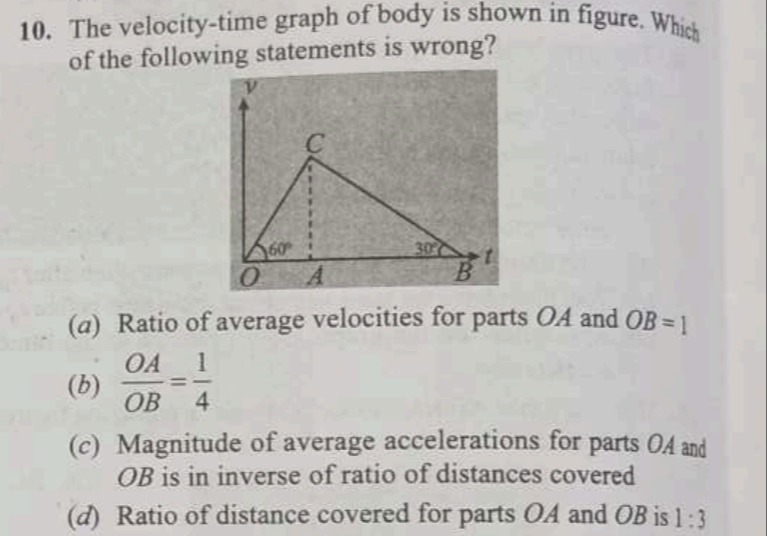
• A. Ratio of average velocities for parts $OA$ and $OB=1$
• B. $\frac{OA}{OB}=\frac{1}{4}$
• C. Magnitude of average accelerations for parts $OA$ and $OB$ is in inverse of ratio of distances covered
• D. Ratio of distance covered for parts $OA$ and $OB$ is $1:3$

Answer 1

Answer: (C)

Magnitude of average accelerations for parts $OA$ and $OB$ is in inverse of ratio of distances covered

Answer 2

Let $t_A$ be the time at point A and $v_{max}$ be the velocity at point C. The slope of OC represents acceleration $a_{OA} = \tan(60^\circ) = \sqrt{3}$. The velocity at C is $v_{max} = a_{OA} \times t_A = \sqrt{3} t_A$. The slope of CB represents acceleration $a_{CB} = \tan(150^\circ) = -\frac{1}{\sqrt{3}}$. The time taken for CB is $t_{CB} = T - t_A$, where $T$ is the total time OB. Using $v_{final} - v_{initial} = a_{CB} \times t_{CB}$, we get $0 - v_{max} = -\frac{1}{\sqrt{3}} (T - t_A)$, so $v_{max} = \frac{T - t_A}{\sqrt{3}}$. Equating expressions for $v_{max}$: $\sqrt{3} t_A = \frac{T - t_A}{\sqrt{3}}$, which gives $4 t_A = T$. Thus, $t_A = \frac{T}{4}$. This means $\frac{OA}{OB} = \frac{t_A}{T} = \frac{1}{4}$. Statement (b) is correct.

The distance covered in OA ($d_{OA}$) is the area of triangle OAC: $d_{OA} = \frac{1}{2} \times OA \times v_{max} = \frac{1}{2} t_A (\sqrt{3} t_A) = \frac{\sqrt{3}}{2} t_A^2$. The time taken for AB is $t_{AB} = T - t_A = 3t_A$. The distance covered in AB ($d_{AB}$) is the area of triangle ACB: $d_{AB} = \frac{1}{2} \times AB \times v_{max} = \frac{1}{2} (3t_A) (\sqrt{3} t_A) = \frac{3\sqrt{3}}{2} t_A^2$. The ratio of distances covered for parts OA and AB is $d_{OA} : d_{AB} = 1:3$. If "parts OA and OB" in statement (d) is interpreted as "parts OA and AB", then statement (d) is correct.

The average velocity for part OA is $v_{avg, OA} = \frac{d_{OA}}{OA} = \frac{\frac{\sqrt{3}}{2} t_A^2}{t_A} = \frac{\sqrt{3}}{2} t_A$. The average velocity for part OB (entire motion) is $v_{avg, OB} = \frac{\text{Total distance}}{\text{Total time}} = \frac{d_{OA} + d_{AB}}{T} = \frac{\frac{\sqrt{3}}{2} t_A^2 + \frac{3\sqrt{3}}{2} t_A^2}{4t_A} = \frac{2\sqrt{3} t_A^2}{4t_A} = \frac{\sqrt{3}}{2} t_A$. The ratio of average velocities for parts OA and OB is $\frac{v_{avg, OA}}{v_{avg, OB}} = 1$. Statement (a) is correct.

For statement (c), if "parts OA and OB" refers to the motion during time interval OA and the entire motion during time interval OB: The magnitude of average acceleration for OA is $|a_{OA}| = |\sqrt{3}| = \sqrt{3}$. The average acceleration for the entire motion OB is $a_{avg, OB} = \frac{v_B - v_O}{T - 0} = \frac{0 - 0}{T} = 0$. The ratio of magnitudes of average accelerations is $\frac{|a_{OA}|}{|a_{avg, OB}|} = \frac{\sqrt{3}}{0}$, which is undefined. The ratio of distances covered for parts OA and OB (entire motion) is $d_{OA} : d_{total} = d_{OA} : (d_{OA} + d_{AB}) = d_{OA} : (d_{OA} + 3d_{OA}) = 1:4$. The inverse ratio of distances covered is $4:1$. The statement claims $\frac{|a_{OA}|}{|a_{avg, OB}|} = \frac{d_{total}}{d_{OA}}$. An undefined quantity cannot equal 4. Thus, statement (c) is wrong under this interpretation.